Sunday Discussion on Biological Issues
The discussion was moderated by John Luecke.
Susan Holmes opened the discussion by suggesting that we might ask the
biologists: what mathematical or biological
questions related to phylogenetic trees are most important to biologists?
She also invited clarifications about things that
have been addressed in talks earlier in the day.
Q. What properties of phylogenetic trees make them different from
random trees? Is there some kind of structure that makes them
different? (Epstein)
- Phylogenetic trees don't look like trees generated by random
branching processes. (Huelsenbeck)
Q. What are the characteristics that a ``distance between trees''
should have that biologists would want? (Luecke)
Q. Is there a difference between some real distribution of trees on tree space
rather than some random distribution? (Holmes)
- Evans: this will help us to construct meaningful confidence sets on trees.
- Felsenstein: Tree spaces are weird. For a cloud of trees, we want to
characterize where in this space those trees are.
Q. Problem: make notions of distances accessible to biologists, so
they might use them. (Huelsenbeck)
- Some comments were made about the use of
methods of Kuhner-Felsenstein, weighted Robinson-Foulds, in biology.
- Diaconis pointed out that in his work on non-standard data
structures, the notions of distances are very useful and basic.
In doing exploratory analyses, they can be useful in
statistical tasks. So, what do biologists think of these distances?
- Holmes pointed out that
how fast MCMC methods converge depends on the geometry of the space,
and the metric chosen.
- Huelsenbeck suggested that a useful task for mathematicians would
be to make some sense of the uses of these distances to biologists?
(such as in an article pitched to biologists).
More comments about tree space topology and branch lengths:
- Huelsenbeck: are there versions of tree space that biologists might
not be
interested in, due to technical conditions? For instance, if
you give a program an alignment, the branches have to be short
enough so that you can align them.
- Felsenstein:
In many cases in biology we are interested in grappling with, such as
origins of mammals, many of the orders seem to have popped up rather quickly.
We could be interested in (a) the branch length and (b) the topology.
When the orders diverged, important things were happening very quickly,
such as morphological changes. But the molecules you are studying may not
have been involved. If you are interested in those morphological
changes, it is important to know what order the branching occurred.
On the other hand, in some other questions, topology many not be as
important as branch length. It really depends on the question you are
asking.
- Sober: A third issue is important: the character states of the
interior nodes of trees.
You might want to know what is the sequence of changes that occurred
on some branch? for instance in some calculation, you may want to
integrate over all possible states of interior nodes.
Felsenstein pointed out that these states on interior nodes are
sometimes overinterpreted-- they are
often viewed as actual states, rather than estimates.
- Penny: in biology, knowing the ``true'' tree may
only be a starting point of the real investigation-- some other
aspect that the biologist is truly interested in. Huelsenbeck gave an
example of an evolution biologist interested in sexual selection.
Although she made a
phylogeny (what she thought was the best tree), she wasn't
primarily interested in the phylogeny, but in further questions about
sexual selection.
Q. How to pick a tree (or tree average) from a set of trees resulting
from data?
- Epstein: in bacteria dna fragments, each one gives a tree.
Which one to use?
Need a tree distance to analyze the resulting 22 different trees.
The distance he used was the BHV metric, but he suspects one obtains
much the same answer with many different tree metrics.
- Evans: this is similar to Mallow's model in statistics,
where you have a distribution on permutations, centered on a
permutation, dropping off in some radial sense. Here, you
have a central tree, and then the probability that you observe some
other tree dies off as you move farther away.
- Penny: one approach to identify ``bad'' portions of
a tree is to try to ``identify the guilty taxon'',
by succedssively removing taxa and then see whether this stabilizes
the tree significantly.
Q. How to understand or deal with residuals, such as non-tree like data?
- Holmes: gave an example in which a friend has a reference tree,
and 8 different plumage trees. In tree space,
if the plumage tree differs from the reference dna tree in some
direction, is that present in the way these things actually evolved?
In statistics, when doing regression, you compare data points to a fitted
line, and ignore the ones that are way off. Here, in tree space,
there's a similar question for non-tree like data:
how much did I have to bend the data to make it into a tree?
- Sober: how do you decide how much off is too much,
before you are worried?
(Scribe's note: this seems to require
a notion of distance not just on tree space,
but some larger space-- such as on the space of DNA sequences-- in which
tree space is embedded. We discussed embedding questions on Wednesday.)
More comments on distances:
- Diaconis told a story where distances fit data remarkably well.
Perception psychologist Roger Shepard studied the visual system, by
showing subjects a configuration of blocks, then some other
configuration, and then asked them: are they are the same?
He found that the time it took people to decide was the
geodesic in the three dimensional rotation group. The data is quite
remarkable, and gave straight line plots. We know what it means to
measure the distance in the rotation group
(but why the brain should know about this is some fascinating
subject in itself.)
- Similarly, does a distance between trees have to have some
interpretation in terms of evolution, in order to be the ``right''
notion of distance?
- Epstein:
For instance, given dna or amino acid sequences, one for each taxon,
this data produces a tree. As sequences change or evolve one
nucleotide at a time, the trees will change. What path does this
trace out in tree space?
(Scribe's note: this appears to require a space of trees that
includes trees with many different numbers of leaves, so that one can
speak of how a tree evolves as species split off from one another.)
- In response to a question,
Felsenstein mentioned a few sources of variation in trees:
(a) statistical error.
(b) coalescence: take a gene copy in three species, and
think of copies ancestral to these. The copies do not come together
instantly, but have some stochastic chance of mixing, and they may
come in some random order that conflicts with a species tree.
(c) horizontal gene transfer.
(Scribe's note: a more detailed discussion of this topic can be found in
Tuesday's discussion.)
Q. Which is better: concatenating DNA sequences first or averaging trees later?
- Holmes: empirical studies show that
if you take all the data and compute one tree, you
generally do less well at
estimating the tree than
than if you take the fragments, use them, then average them.
This comes from the CAT(0) property.
The intuition behind it
is if you average in a negatively curved space, you converge much
faster than you should.
- St. John: pointed out an example with
20 simulated DNA sequences: if
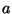 is one part of the genome, and
is one part of the genome, and 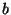 is
another part, then the trees obtained from using
is
another part, then the trees obtained from using 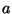 combined with
combined with 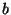 do
not overlap, and are somewhat in between, the trees obtained from
do
not overlap, and are somewhat in between, the trees obtained from 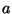 and from
and from 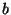 alone. Felsenstein commented that the stochastic effects
pushed
alone. Felsenstein commented that the stochastic effects
pushed 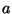 and
and 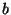 in different directions in tree space.
in different directions in tree space.
She also noted that in studying hybridization (e.g., sunflowers),
she was surprised that she
didn't get more overlap, and often the right answer was with
part of the data, not all the data.
- Felsenstein: Biologists are in disagreement about whether
concatenating or averaging is better. Statistically, which is better?
- It was pointed out that a paper by Cunningham (1997) does comparisons.
Also, work by Amit, and statistical literature on boosting and bagging.
- Billera: there's a notion of equivalent metrics in topology, and any
of these will do. (In doing geometry, where issues like curvature come
into play, the choice of metrics is important.) It may be the case
that even though certain metrics are good enough for some purposes, it
doesn't mean that other metrics aren't valid.
Q. What is the right notion of an ``average'' of trees?
- The biologists present agreed that this was a very interesting
question for biologists.
- Vert: Two important ideas emerge when working with decision trees:
(1) average decrease some variance, (2) averaging can leave the space.
Boosting will leave the space, if we don't leave the space it's really
not boosting. The averaging we are discussing here doesn't leave the
space of trees.
- More discussion on averaging took place here. Holmes made a comment
about the ``non-associativity'' of trees (related to considering trees
of trees, when building trees one character at a time). Billera made
some remarks about how averaging may be better than concatenation, but
we have no guarantee that it is any good.
- Penny discussed the notion of a median tree:
the tree that is closest on average to all the others.
- Felsenstein: other examples are the consensus tree, and
majority rule consensus tree.
Q. What are good properties of averaging? (Luecke)
Q. What would be the distribution on trees that gives majority rule
consensus as its average? (Holmes)
- Holmes: would like any tree average to be
an expected value with respect to some distribution on tree space.
Back to the
main index
for Geometric models of biological phenomena.