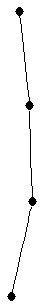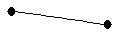Graph catalog: Spectra of small graphs
Index of graphs
Main Index
Index of graphs
Description of graph entries
Graph operation
Parameter relationships
References
The catalog
This catalog provides information about the minimum rank and other graph
parameters for families of connected graphs. The description of a family
of graphs involves one or more parameters (often the order n of the
graph).
For families, please see the
families catalog.
For general background on the minimum
rank problem, please see [FH]. Proofs of
the results in the catalog can be found in the references
cited in the catalog.
This catalog was developed through the American Institute of Mathematics
workshop, "Spectra of Families of Matrices described by Graphs, Digraphs,
and Sign Patterns," and is hosted by the AIM web-site. It is edited by
Jason Grout, Leslie Hogben, Hein van der Holst and Amy Wangsness.
The web-page was designed by David Farmer.
Please refer any questions or comments about the content of the catalog,
including corrections or suggestions for additional information, to
Leslie Hogben (lhogben(())iastate.edu).
Please refer any questions or comments about the operation of this web-site
to David Farmer (farmer(())aimath.org).
AIM workshop participants:
Francesco Barioli, Wayne Barrett, Avi Berman,
Richard Brualdi, Steven Butler,
Sebastian Cioaba, Dragos Cvetkovic, Jane Day,
Louis Deaett, Luz DeAlba, Shaun Fallat, Shmuel Friedland,
Chris Godsil, Jason Grout, Willem Haemers, Leslie Hogben,
In-Jae Kim, Steve Kirkland, Raphael Loewy, Judith McDonald,
Rana Mikkelson,
Sivaram Narayan, Olga Pryporova, Uri Rothblum, Irene Sciriha,
Bryan Shader, Wasin So, Dragan Stevanovic, Pauline van den Driessche,
Hein van der Holst, Kevin Vander Meulen, Amy Wangsness, Amy Yielding.
Entries in the catalog
A typical entry in this catalog includes the following information
for the graph or family of graphs.
| Symbol name |
Common names/symbols are used to describe a graph G in the family.
Sometimes a graph operation is used.
|
|
picture |
A picture of the graph, or a representative example from the family.
|
|
graph6 | Code describing the adjacency matrix.
|
| order | The number of vertices in the graph
|
| mr |
For a real symmetric matrix A, the graph of A,
denoted G(A), is the graph with vertices
{1,...,n } and edges { {i,j } | aij ≠ 0 and i
≠ j }
(note that the diagonal of A is ignored in determining G(A)).
The minimum rank of G is
mr(G)=min{rank(A) : A ∈ Rn, AT=A, and G(A)=G}.
|
| M |
The maximum nullity (= maximum multiplicity of an eigenvalue) of a real symmetric matrix A such that G(A)=G
|
| field independent |
Minimum rank can be defined for symmetric matrices over any field. ``Yes" means the minimum rank of G is the same for all fields.
|
| ξ |
A real symmetric matrix M satisfies the Strong Arnold
Hypothesis provided there does not exist a nonzero symmetric matrix
X satisfying:
- MX = 0,
- M ° X = 0,
- I ° X=0,
where ° denotes the Hadamard (entrywise) product and I is the identity matrix.
The Colin de Veriere-type parameter ξ(G) is the maximum multiplicity of 0 as an eigenvalue
among matrices symmetric real matrices that satisfy
- G(A )=G and
- A satisfies the Strong Arnold Hypothesis.
|
| ω |
The largest value of m for which a clique of order m (subgraph isomorphic to Km) is called the clique number of G
and denoted by ω(G).
|
| δ |
The minimum degree of a vertex of G is denoted by δ(G).
|
| tw |
A tree-decomposition of a graph G=(V,E) is a pair
(T,W), where T is a tree and W={Wt : t∈ V(T)} is a family of subsets of V
with the properties:
- ∪ {Wt : t∈ V(T)}=V,
- for every edge e∈ E, there is a t∈V(T) such that has both ends of e are in Wt, and
- if t1,t2,t3∈ V(T)
and t2 lies on the path from t1 to t3 in T, then
Wt1∩Wt3⊆Wt2.
The width of a tree-decomposition is
max{|Wt| - 1 : t∈ V(T)}. The tree-width of G, denoted by tw(G), is the minimum possible width of a tree-decomposition of G.
|
| cc |
Clique covering number, or Cliquecover.
A set of subgraphs of G, each of which is a clique and such that every edge of G is
contained in at least one of these cliques, is called a clique covering of G.
The clique covering number of G, denoted by cc(G), is the smallest number of
cliques in a clique covering of G.
|
| diam |
The distance between two vertices in a graph G is the
number of edges in a shortest path between them.
The diameter of G, diam(G), is the maximum distance between any two vertices
of G.
|
| maxinducedpath |
The maximum number of edges in a path that is an induced subgraph of G.
|
| Z |
Color-change rule:
If G is a graph with each vertex colored either white or black, u is a black vertex of G, and exactly one neighbor v of u is white, then change the color of v to black.
Given a coloring of G, the derived coloring is the result of applying the color-change rule until no more changes result.
A zero forcing set for a graph G is a subset of vertices Z such that if initially the vertices in Z are colored black and the remaining vertices are colored white, the derived coloring of G is all black.
Z(G) is the minimum of ord Z over all zero forcing sets Z⊆ V(G).
|
| α |
An induced subgraph H of a graph G
is a coclique or independent set of vertices
if H has no edges.
The largest value of m for which a coclique with m
vertices exists is called the vertex independence number
of G and denoted by α(G).
|
|
| Notes: |
Any other comments.
|
Graph operations
The following graph operations are used to construct families:
- The complement of a graph G=(V,E) is the
graph G‾=(V,E‾), where E‾
consists of all two element sets from V that are not in E.
- The line graph of a graph G=(V,E), denoted L(G), is the graph having vertex set E, with two vertices in L(T) adjacent if and only if the corresponding edges are adjacent in T.
- The Cartesian product of two graphs G and H,
denoted G ☐ H,
is the graph with vertex set V(G) × V(H) such that
(u,v) is adjacent to (u',v') if and only if
(1) u=u' and vv' ∈ E(H),
or
(2) v=v' and uu' ∈ E(G).
- The strong product of two graphs G and H, denoted
G ⊠ H, is the graph with vertex set V(G) × V(H) such
that (u,v) is adjacent to (u',v') if and only if
(1) uu' ∈ E(G)
and vv' ∈ E(H),
or
(2) u=u' and vv' ∈ E(H),
or
(3) v=v'
and uu' ∈ E(G).
- The corona of G with H, denoted
G ° H, is the graph of order |G||H| + |G|
obtained by taking one copy of G and |G| copies
of H, and joining all the vertices in the ith
copy of H to the ith vertex of G.
Parameter Relationships
The following relationships between the parameters are known:
- mr(G) + M(G) = ord G (where ord G denotes the order of G)
- M(G) ≤ Z(G) [AIM]
- ξ(G) ≤ M(G) [BFH3]
- ω(G) -1 ≤ ξ(G) [BFH3]
- δ(G) ≤ tw(G)
- mr(G) ≤ cc(G)
- diam(G) ≤ inpath(G) ≤ mr(G)
- ξ(G) ≤ ord G - α(G) + 1 [BFH3]
References
[AIM] AIM Minimum rank - special graphs work group. Zero forcing sets and the minimum rank of graphs. Preprint.
[BFH] F. Barioli, S. Fallat, and L. Hogben.
Computation of minimal rank and path cover number for graphs.
Linear Algebra and Its Applications,
392: 289--303, 2004.
[BFH2] F. Barioli, S. Fallat, and L. Hogben.
On the difference between the maximum multiplicity and path cover number for
tree-like graphs.
Linear Algebra and Its Applications 409: 13--31, 2005.
[BFH3] F. Barioli, S. Fallat, and L. Hogben.
A variant on the graph parameters of Colin de Verdi`ere:
Implications to the minimum rank of graphs.
Electronic Journal of Linear Algebra,
13: 387--404, 2005.
[BHL] W. Barrett, H. van der Holst and R. Loewy.
Graphs whose minimal rank is two.
Electronic Journal of Linear Algebra,
11: 258--280, 2004.
[FH] S. Fallat and L. Hogben.
The Minimum Rank of Symmetric Matrices Described by a Graph: A Survey. Preprint.
[H] L. Hogben.
Spectral graph theory and the inverse eigenvalue problem of a
graph.
Electronic Journal of Linear Algebra, 14:12-31, 2005.
[HvdH] L. Hogben and H. van der Holst.
Forbidden minors for the class of graphs G with
ξ(G) ≤ 2. To appear in Linear Algebra and Its Applications.
[JLD] C. R. Johnson and A. Leal Duarte.
The maximum multiplicity of an eigenvalue in a matrix whose graph is a tree.
Linear and Multilinear Algebra 46: 139--144, 1999.
[JS] C. R. Johnson and C. M. Saiago.
Estimation of the maximum multiplicity of an eigenvalue in terms of the vertex degrees
of the graph of the matrix.
Electronic Journal of Linear Algebra,
9:27--31, 2002.
Catalog of graphs
 Path on 5 vertices
Path on 5 vertices |
| graph6 : | DhC | | Order : | 5 | | mr : | 4 | | M : | 1 | | field independent : | yes | | ξ : | 1 | | ω : | 2 | | δ : | 1 | | tw : | 1 | | cliquecover : | 4 | | Diameter : | 4 | | maxinducedpath : | 4 | | α : | 3 | | G name : | G31 | | Notes : | G31
|
| 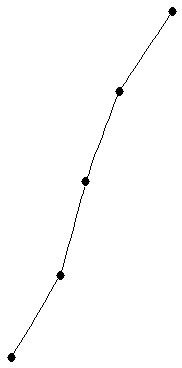 |
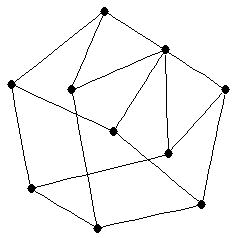
| Peterson graph |
| graph6 : | IheA@GUAo | | Order : | 10 | | mr : | 5 | | M : | 5 | | δ : | 3 | | Z : | 5 | | Notes : | Reference: [AIM]
|
|  |
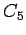 5-cycle
5-cycle |
| graph6 : | Dhc | | Order : | 5 | | mr : | 3 | | M : | 2 | | field independent : | yes | | ξ : | 2 | | ω : | 2 | | δ : | 2 | | tw : | 2 | | cliquecover : | 5 | | Diameter : | 2 | | maxinducedpath : | 3 | | α : | 2 | | G name : | G38 | | Notes : | G38
|
|  |
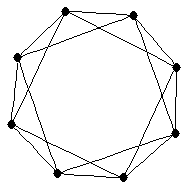
| 4-antiprism |
| graph6 : | GzK[]K | | Order : | 8 | | mr : | 4 | | M : | 4 | | ξ : | 4 | | ω : | 3 | | δ : | 4 | | Z : | 4 | | Notes : | Reference: [AIM]
|
|  |
| Chair or Generalized star on 5 vertices |
| graph6 : | DsC | | Order : | 5 | | mr : | 3 | | M : | 2 | | field independent : | yes | | ξ : | 2 | | ω : | 2 | | δ : | 1 | | tw : | 1 | | cliquecover : | 4 | | Diameter : | 3 | | maxinducedpath : | 3 | | α : | 3 | | G name : | G30, tree | | Notes : | G30, tree
|
| 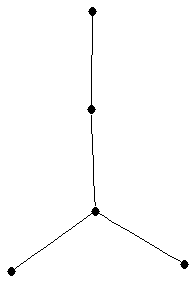 |
| Fish |
| graph6 : | DXK | | Order : | 5 | | mr : | 3 | | M : | 2 | | field independent : | yes | | ξ : | 2 | | ω : | 3 | | δ : | 1 | | tw : | 2 | | cliquecover : | 3 | | Diameter : | 2 | | maxinducedpath : | 2 | | α : | 3 | | G name : | G34 | | Notes : | forbidden for mr=2
|
| 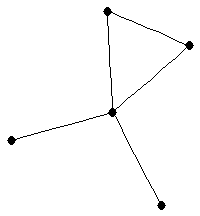 |
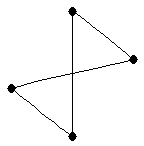
| |
| graph6 : | DhK | | Order : | 5 | | mr : | 3 | | M : | 2 | | δ : | 1 | | G name : | G36 | | Notes : | G36
|
|  |
| |
| graph6 : | DhS | | Order : | 5 | | mr : | 3 | | M : | 2 | | δ : | 1 | | G name : | G37 | | Notes : | G37
|
| 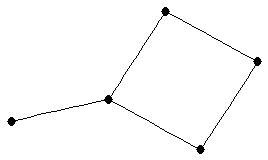 |
| |
| graph6 : | Dh[ | | Order : | 5 | | mr : | 3 | | M : | 2 | | δ : | 1 | | G name : | G41 | | Notes : | G41
|
| 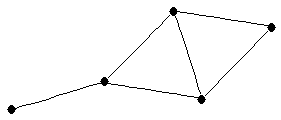 |
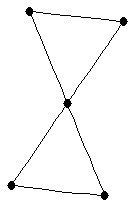
| |
| graph6 : | Dj[ | | Order : | 5 | | mr : | 2 | | M : | 3 | | δ : | 1 | | G name : | G45 | | Notes : | G45
|
| 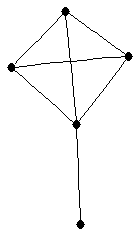 |
| Dart |
| graph6 : | DjS | | Order : | 5 | | mr : | 3 | | M : | 2 | | field independent : | yes | | ξ : | 2 | | ω : | 3 | | δ : | 1 | | tw : | 2 | | cliquecover : | 3 | | Diameter : | 2 | | maxinducedpath : | 2 | | α : | 3 | | G name : | G40, forbidden for mr=2 | | Notes : | G40, forbidden for mr=2
|
| 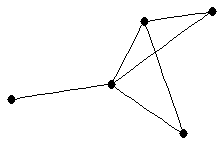 |
| bull |
| graph6 : | Dgs | | Order : | 5 | | mr : | 3 | | M : | 2 | | δ : | 1 | | G name : | G35 | | Notes : | G35
|
| 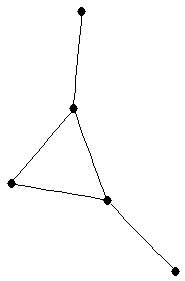 |
| house |
| graph6 : | Dhs | | Order : | 5 | | mr : | 3 | | M : | 2 | | field independent : | yes | | ξ : | 2 | | ω : | 3 | | δ : | 2 | | tw : | 2 | | cliquecover : | 4 | | Diameter : | 2 | | maxinducedpath : | 3 | | α : | 2 | | G name : | G43 | | Notes : | G43, linear 2-tree
|
| 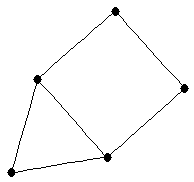 |
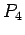 Path on 4 vertices
Path on 4 vertices |
| graph6 : | Ch | | Order : | 4 | | mr : | 3 | | M : | 1 | | δ : | 1 | | G name : | G14 | | Notes : | G14
|
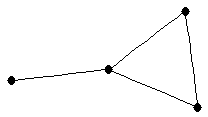
| 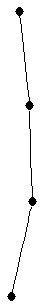 |
| |
| graph6 : | Cj | | Order : | 4 | | mr : | 2 | | M : | 2 | | δ : | 1 | | G name : | G15 | | Notes : | G15
|
|  |
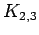
|
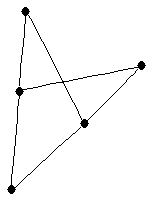
| graph6 : | DlS | | Order : | 5 | | mr : | 2 | | M : | 3 | | δ : | 2 | | G name : | G44 | | Notes : | G44
|
|  |
| |
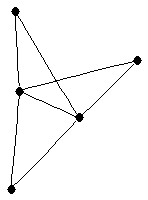
| graph6 : | DnS | | Order : | 5 | | mr : | 2 | | M : | 3 | | δ : | 2 | | G name : | G46 | | Notes : | G46
|
|  |
| |
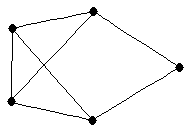
| graph6 : | Dls | | Order : | 5 | | mr : | 2 | | M : | 3 | | δ : | 2 | | G name : | G48 | | Notes : | G48
|
|  |
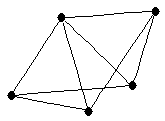
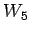 Wheel
Wheel |
| graph6 : | Dl{ | | Order : | 5 | | mr : | 2 | | M : | 3 | | δ : | 3 | | G name : | G50 | | Notes : | G50
|
|  |
| Wheel |
| graph6 : | Dl{ | | Order : | 5 | | mr : | 2 | | M : | 3 | | δ : | 3 | | G name : | G50 | | Notes : | G50
|
|  |
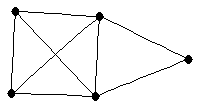
| |
| graph6 : | Dns | | Order : | 5 | | mr : | 2 | | M : | 3 | | δ : | 2 | | G name : | G49 | | Notes : | G49
|
|  |
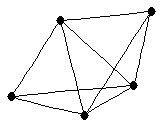
| K_5 - e |
| graph6 : | Dn{ | | Order : | 5 | | mr : | 2 | | M : | 3 | | δ : | 3 | | G name : | G51 | | Notes : | G51
|
|  |
 4-cycle
4-cycle |
| graph6 : | Cl | | Order : | 4 | | mr : | 2 | | M : | 2 | | δ : | 2 | | G name : | G16 | | Notes : | G16
|
|  |
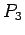 ,
, 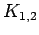 Path on 3 vertices
Path on 3 vertices |
| graph6 : | Bg | | Order : | 3 | | mr : | 2 | | M : | 1 | | field independent : | yes | | ω : | 2 | | δ : | 1 | | tw : | 1 | | cliquecover : | 2 | | Diameter : | 2 | | maxinducedpath : | 2 | | α : | 2 | | G name : | G6 | | Notes : | G6
|
|  |
| |
| graph6 : | DxK | | Order : | 5 | | mr : | 2 | | M : | 3 | | δ : | 2 | | G name : | G42 | | Notes : | G42
|
|  |
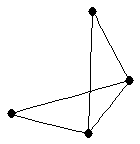
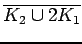 Diamond
Diamond |
| graph6 : | Cz | | Order : | 4 | | mr : | 2 | | M : | 2 | | field independent : | yes | | ω : | 3 | | δ : | 2 | | tw : | 2 | | cliquecover : | 2 | | Diameter : | 2 | | maxinducedpath : | 2 | | α : | 2 | | G name : | G17 | | Notes : | G17
|
|  |
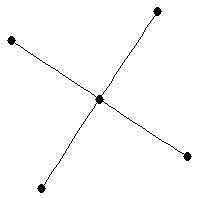
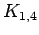 Star on 5 vertices
Star on 5 vertices |
| graph6 : | Ds_ | | Order : | 5 | | mr : | 2 | | M : | 3 | | δ : | 1 | | G name : | G29 | | Notes : | G29
|
|  |
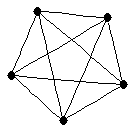
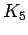 Complete graph on 5 vertices
Complete graph on 5 vertices |
| graph6 : | D~{ | | Order : | 5 | | mr : | 1 | | M : | 4 | | δ : | 4 | | G name : | G52 | | Notes : | G52
|
|  |
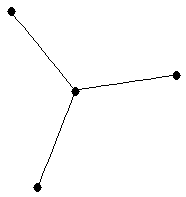
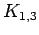 Star on 4 vertices
Star on 4 vertices |
| graph6 : | Cs | | Order : | 4 | | mr : | 2 | | M : | 2 | | δ : | 1 | | G name : | G13 | | Notes : | G13
|
|  |
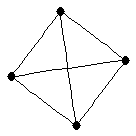
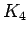 Complete graph on 4 vertices
Complete graph on 4 vertices |
| graph6 : | C~ | | Order : | 4 | | mr : | 1 | | M : | 3 | | δ : | 3 | | G name : | G18 | | Notes : | G18
|
|  |
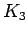 ,
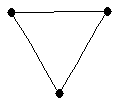
, 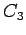 Complete graph on 3 vertices
Complete graph on 3 vertices |
| graph6 : | Bw | | Order : | 3 | | mr : | 1 | | M : | 2 | | field independent : | yes | | ω : | 3 | | δ : | 2 | | tw : | 2 | | cliquecover : | 1 | | Diameter : | 1 | | maxinducedpath : | 1 | | α : | 1 | | G name : | G7 | | Notes : | G7
|
|  |
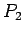 ,
, 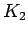 Complete graph on 2 vertices
Complete graph on 2 vertices |
| graph6 : | A_ | | Order : | 2 | | mr : | 1 | | M : | 1 | | δ : | 1 | | G name : | G3 | | Notes : | G3
|
| 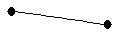 |