These are
geometrically defined intermediate subvarieties between
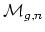 and
and
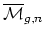 whose topology and tautological rings may also have a nice
structure. They include the moduli space
whose topology and tautological rings may also have a nice
structure. They include the moduli space
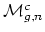 of curves of
compact type (i.e.
of curves of
compact type (i.e.
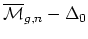 , or those curves whose dual
graph is a tree),
, or those curves whose dual
graph is a tree),
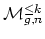 (curves with
(curves with 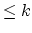 rational
components), and
rational
components), and
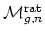 (curves consisting of a
single genus
(curves consisting of a
single genus 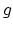 component attached to trees of rational tails).
component attached to trees of rational tails).
Jeffrey Herschel Giansiracusa
2005-06-27