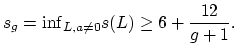The slope conjecture is about the possible
homology classes of hypersurfaces in the moduli space of curves.
Given an effective line bundle 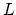 on
on
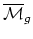 , we can find
non-negative
, we can find
non-negative 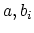 for which
where
for which
where 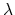 is the Hodge class
is the Hodge class
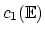 and
and
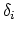 is the class Poincare-dual to the
boundary divisor
is the class Poincare-dual to the
boundary divisor
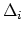 . The slope of the divisor
. The slope of the divisor 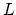 is
is
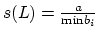 . The slope conjecture states that
For
. The slope conjecture states that
For
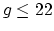 this would imply that the Kodaira dimension of
this would imply that the Kodaira dimension of
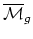 is
is
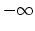 . As it happens, Farkas and Popa have recently constructed
several counterexamples to the slope conjecture. However, one can
still ask for other weaker lower bounds on
. As it happens, Farkas and Popa have recently constructed
several counterexamples to the slope conjecture. However, one can
still ask for other weaker lower bounds on 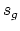 . It is known that
. It is known that
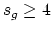 .
.
Jeffrey Herschel Giansiracusa
2005-06-27