The moduli space of maps
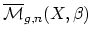 is highly singular, and yet it has a homology
class which behaves much like a fundamental class, and is hence called
the virtual fundamental class
is highly singular, and yet it has a homology
class which behaves much like a fundamental class, and is hence called
the virtual fundamental class
![$ [\overline{\mathcal{M}}_{g,n}(X,\beta)]^{\mathrm{vir}}$](img211.png) defined in terms of the
deformation theory of stable maps to
defined in terms of the
deformation theory of stable maps to 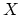 .
The Gromov-Witten
invariants of
.
The Gromov-Witten
invariants of 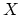 are defined by integrating various geometric cohomology
classes over this class.
are defined by integrating various geometric cohomology
classes over this class.
Jeffrey Herschel Giansiracusa
2005-06-27