The Deligne-Mumford compactification is obtained as a moduli space for
stable genus g curves with marked points, (instead of considering just
smooth curves, as in
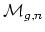 ). A stable genus
). A stable genus 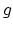 curve is a
connected, projective curve with at worst nodal singularities and
finite automorphism group. This translates to: every genus 0
irreducible component has at least three marked or nodal points and
every genus 1 component has at least one marked or nodal point. This
space is important because it is a smooth compactification (as a
stack, at least) with easy-to-understand boundary components that give
an inductive structure to all the moduli spaces of curves. For
instance, Deligne and Mumford used this compactification to prove that
curve is a
connected, projective curve with at worst nodal singularities and
finite automorphism group. This translates to: every genus 0
irreducible component has at least three marked or nodal points and
every genus 1 component has at least one marked or nodal point. This
space is important because it is a smooth compactification (as a
stack, at least) with easy-to-understand boundary components that give
an inductive structure to all the moduli spaces of curves. For
instance, Deligne and Mumford used this compactification to prove that
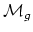 is irreducible for any characteristic.
is irreducible for any characteristic.
Jeffrey Herschel Giansiracusa
2005-06-27