The primality testing algorithm we present is based upon the following identity: ![]() is prime if and only if
is prime if and only if
Conjecture. To prove that ![]() is prime, it is enough to let
is prime, it is enough to let ![]() run over the set
run over the set
We were unable to prove this conjecture, but, instead the modified conjecture, which is then a proposition:
Proposition. [Modified conjecture]
To prove that ![]() is prime, it is enough to let
is prime, it is enough to let ![]() run over the set
run over the set
Remark.
One can replace the assumption that ![]() does not have a small prime factor by adding to the list the polynomials
does not have a small prime factor by adding to the list the polynomials ![]() .
.
For a fixed ![]() , this gives only that
, this gives only that ![]() is a prime power, which is a condition readily checked.
is a prime power, which is a condition readily checked.
We now prove the modified conjecture.
If ![]() is prime, clearly all of these conditions will hold.
is prime, clearly all of these conditions will hold.
Assume that ![]() is composite and does not have a `small' prime factor. Assume that
is composite and does not have a `small' prime factor. Assume that
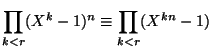
Suppose
![]() for
for ![]() a prime. Then
a prime. Then
![]() (
(![]() does not have a small prime divisor) so
does not have a small prime divisor) so
![]() as the group is cyclic. Therefore
as the group is cyclic. Therefore
![]() for all
for all
![]() . A simple counting argument (look at all of the possible numbers whose prime divisors are all smaller than
. A simple counting argument (look at all of the possible numbers whose prime divisors are all smaller than
![]() , the identity holds for them but there are more than
, the identity holds for them but there are more than ![]() of them) shows that this cannot happen.
of them) shows that this cannot happen.
Assume that ![]() is composite but not a prime power. Let
is composite but not a prime power. Let ![]() ,
, ![]() prime, and fix
prime, and fix ![]() . Now:
. Now:
Claim. We have
This can be seen by replacing ![]() by
by ![]() as appropriate.
as appropriate.
Definition.
A number ![]() is introspective for
is introspective for ![]() if
if
Both ![]() and
and ![]() are introspective for
are introspective for ![]() ,
,
![]() . Indeed, a prime
. Indeed, a prime ![]() is trivially introspective for every polynomial.
is trivially introspective for every polynomial.
Observe that if ![]() and
and ![]() are introspective for
are introspective for ![]() , then so is
, then so is ![]() . This is clear as
. This is clear as
Now let
![]() and
and
Let ![]() be the order of the group generated by
be the order of the group generated by ![]() and
and ![]() in
in
![]() . There are
. There are ![]() elements in
elements in ![]() less than or equal to
less than or equal to
![]() .
.
Furthermore, there are
![]() distinct polynomials of degree
distinct polynomials of degree ![]() which are distinct modulo
which are distinct modulo ![]() and
and ![]() , where
, where ![]() is an irreducible factor of the
is an irreducible factor of the ![]() th cyclotomic polynomial in
th cyclotomic polynomial in
![]() . We show this as follows.
. We show this as follows.
The number of polynomials in ![]() of degree
of degree ![]() is at least
is at least
![]() by simply considering products of distinct linear factors in
by simply considering products of distinct linear factors in ![]() . Assume that
. Assume that
![]() and
and
![]() . (We will come back to this: we can choose the value of
. (We will come back to this: we can choose the value of ![]() to obtain it.) Then
to obtain it.) Then
Let
![]() ,
,
![]() and
and
![]() ; this is possible as
; this is possible as ![]() is the order of the group generated by
is the order of the group generated by ![]() and
and ![]() in
in
![]() . Let
. Let
![]() be of degree
be of degree ![]() . Then
. Then
Finally, we show that
![]() and
and
![]() . Suppose the order of
. Suppose the order of ![]() is
is
![]() in
in
![]() . Then
. Then
![]() . Now use the fact that the least common multiple of the first
. Now use the fact that the least common multiple of the first ![]() numbers is at least
numbers is at least ![]() .
.
It is easy to see that this algorithm has runtime
![]() .
.
Back to the
main index
for Future directions in algorithmic number theory.