Consider the following problem: Given a prime ![]() and an integer
and an integer ![]() , find an irreducible polynomial
, find an irreducible polynomial
![]() of degree
of degree ![]() . And do so in time polynomial in
. And do so in time polynomial in ![]() and
and ![]() . There is a randomized algorithm which attacks this problem by picking a polynomial at random (approximately
. There is a randomized algorithm which attacks this problem by picking a polynomial at random (approximately ![]() out of every
out of every ![]() polynomials will be irreducible), and testing each for irreducibility (which is fast), continuing this procedure until you find one, then stop. But we are interested here in a deterministic algorithm. Already for
polynomials will be irreducible), and testing each for irreducibility (which is fast), continuing this procedure until you find one, then stop. But we are interested here in a deterministic algorithm. Already for ![]() , this is a difficult problem, equivalent to finding a quadratic nonresidue modulo
, this is a difficult problem, equivalent to finding a quadratic nonresidue modulo ![]() .
.
Assuming the ERH, Adleman and Lenstra have a solution to this problem. Unconditionally, they also find an irreducible polynomial of degree ![]() with
with
![]() , where
, where ![]() is an effectively computable number. Letting
is an effectively computable number. Letting
![]() and
and ![]() (where you do not know a priori if
(where you do not know a priori if ![]() is prime), the polynomial produced has degree
is prime), the polynomial produced has degree
![]() , and the runtime of the AKS algorithm becomes
, and the runtime of the AKS algorithm becomes
![]() . We improve this theorem to the following:
. We improve this theorem to the following:
Theorem. Such a polynomial can be produced with
![]() for
for ![]() sufficiently large and
sufficiently large and
![]() .
.
The bound for the `sufficiently large' part depends effectively on the choice of ![]() .
.
Theorem. There is an effectively computable function
![]() and a deterministic algorithm such that if
and a deterministic algorithm such that if
![]() ,
,
![]() , and
, and
![]() , the algorithm produces pairs
, the algorithm produces pairs
![]() such that for each
such that for each ![]() ,
, ![]() is prime,
is prime, ![]() ,
,
![]() , the order of
, the order of
![]() modulo
modulo ![]() is
is ![]() . Further, the
. Further, the
![]() are pairwise coprime, and
are pairwise coprime, and
![]() . This algorithm runs in time
. This algorithm runs in time
![]() .
.
Let ![]() be the Gaussian period of degree
be the Gaussian period of degree ![]() in
in
![]() (the trace of
(the trace of
![]() into the unique subfield of degree
into the unique subfield of degree ![]() over
over
![]() ). The element
). The element
![]() has degree
has degree
![]() over the rationals (by coprimality). If
over the rationals (by coprimality). If ![]() is prime, and if
is prime, and if ![]() is the minimal polynomial of
is the minimal polynomial of ![]() then
then ![]() is irreducible over
is irreducible over
![]() . Checking if
. Checking if
![]() in
in
![]() (together with some other conditions), we see that
(together with some other conditions), we see that ![]() gives rise to a pseudofield.
gives rise to a pseudofield.
Let
![]() . Throughout, we assume that
. Throughout, we assume that ![]() is `sufficiently large' with the bound being effectively computable, depending only on the choice of
is `sufficiently large' with the bound being effectively computable, depending only on the choice of ![]() .
.
Proposition. All but
![]() primes
primes ![]() have a prime
have a prime
![]() with
with
![]() and the order of
and the order of
![]() modulo
modulo ![]() is equal to
is equal to ![]() .
.
Therefore up to ![]() , almost all of the primes are useful in the context of our theorem. This proposition is a natural extension of the argument in the original AKS paper, together with an added ingredient about the distribution of primes
, almost all of the primes are useful in the context of our theorem. This proposition is a natural extension of the argument in the original AKS paper, together with an added ingredient about the distribution of primes ![]() such that
such that ![]() is smooth due to Pomerance and Shperlinski.
is smooth due to Pomerance and Shperlinski.
Proposition. Let ![]() be a set of primes
be a set of primes ![]() with
with
![]() and
and
![]() . Then there are
. Then there are
![]() primes
primes ![]() such that
such that ![]() is free of primes from
is free of primes from
![]() .
.
This proposition follows from a method of Balog, together with some effective estimates on the distribution of primes in residue classes. Together, these two propositions give the corollary:
Corollary. Let ![]() be the set of primes
be the set of primes ![]() in the first proposition satisfying
in the first proposition satisfying
![]() . Then
. Then
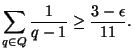
Proposition. There exists a subset of ![]() in the corollary with product in the interval
in the corollary with product in the interval ![]() .
.
The proof of this theorem relies upon combinatorial number theory (essentially, you can solve a bin packing problem using the primes ![]() ). It relies upon:
). It relies upon:
Theorem. [Continuous Frobenius theorem]
If ![]() is an open subset of
is an open subset of
![]() ,
, ![]() is closed under addition, and
is closed under addition, and
![]() , then for any
, then for any ![]() ,
,
![]() , the
, the ![]() measure of
measure of
![]() is
is ![]() , i.e.
, i.e.
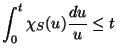
Now a remark about effectivity. It was proven by de la Vallée Poussin in 1896 that
Now we give an outline of the proof of the Frobenius theorem. First, it is sufficient to prove the case where
![]() (i.e.
(i.e. ![]() contains only finitely many intervals). Second, since
contains only finitely many intervals). Second, since
![]() , for all
, for all
![]() either
either
![]() or
or
![]() (*). Now fix
(*). Now fix
![]() such that
such that
![]() and consider all sets
and consider all sets
![]() satisfying
satisfying
![]() (**) as well as condition (*). Under these conditions, there exists a maximum to
(**) as well as condition (*). Under these conditions, there exists a maximum to
![]() . We may thus assume that
. We may thus assume that
![]() is a maximum. We show in the paper that we can assume that
is a maximum. We show in the paper that we can assume that
![]() .
.
Let
![]() with
with
![]() . Let
. Let
![]() . For all
. For all
![]() and
and
![]() ,
,
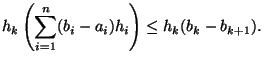
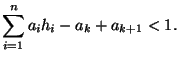
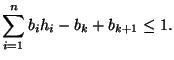
Let
![]() such that
such that ![]() for all
for all ![]() . Then there exists
. Then there exists
![]() such that for all
such that for all
![]() ,
,
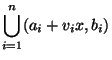
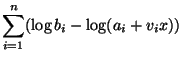
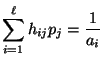
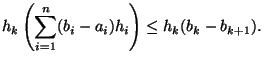
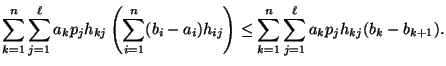
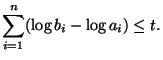
Back to the
main index
for Future directions in algorithmic number theory.