Silverberg: Applications of Algebraic Tori to Crytography

In this lecture we discuss `torus-based cryptography', and counterexamples to conjectures in an article entitled Looking Beyond XTR, and compare TBC with Lucas-based cryptosystems and XTR, and understand LUC, XTR, and Beyond in terms of algebraic tori. This is joint work with Karl Rubin, and inspired by XTR.

The cryptosystem XTR (due to A. Lenstra and E. Verheul) concerns the extension $\mathbb{F}_{p^6}/\mathbb{F}_{p^2}$: they consider the subgroup of $\mathbb{F}_{p^6}^*$ of order $p^2-p+1$ with generator $g$; the public knowledge is ${\mathrm{Tr}}_{\mathbb{F}_{p^6}/\mathbb{F}_{p^2}}(g)$, what is shared is ${\mathrm{Tr}}_{\mathbb{F}_{p^6}/\mathbb{F}_{p^2}}(g^{ab})$, where ${\mathrm{Tr}}(g^a)$ and ${\mathrm{Tr}}(g^b)$ are transmitted. In this setup, you get the security of $\mathbb{F}_{p^n}^*$ while transmitting only $\phi(n)$ elements of $\mathbb{F}_{p}$.

Let $L/k$ be a finite cyclic extension with intermediate field $F$. Let $g \in L \setminus F$, and denote by $C_g$ the ${\mathrm{Gal}}(L/F)$-conjugacy class of $g$, so the characteristic polynomial of $g$ over $F$ is $\prod_{h \in C_g}(X-h)$. For $L=\mathbb{F}_{p^6}$, $F=\mathbb{F}_{p^2}$, $k=\mathbb{F}_p$, the polynomial is $x^3-s_1x^2+s_2x-s_3$, where $s_1={\mathrm{Tr}}_{L/F}(g)$, $s_3=N_{L/F}(g)$, and $s_2={\mathrm{Tr}}_{L/F}(gg^\sigma)$, where $\langle \sigma \rangle ={\mathrm{Gal}}(L/F)$. If $g$ is in the subgroup of $L^*$ of order $p^2-p+1$, then $s_3=1$ and $s_2={\mathrm{Tr}}_{L/F}(g)^p$. Therefore knowing ${\mathrm{Tr}}_{L/F}(g)$ is equivalent to knowing all the symmetric polynomials on $C_g$ which is equivalent to knowing $C_g$ as a set, so you know $C_{g^a}$ and this is equivalent to knowing ${\mathrm{Tr}}_{L/F}(g^a)$. In other words, you can exponentiate, but you cannot multiply: ${\mathrm{Tr}}(g)$ and ${\mathrm{Tr}}(h)$ do not determine ${\mathrm{Tr}}(gh)$; i.e. knowing $C_g$ and $C_h$ does not allow you to know $C_{gh}$.

Bosma-Hutton-Verheul conjecture that for all $n$, there exists a divisor $d \mid n$ such that $d \mid \phi(n)$ and for $L=\mathbb{F}_{p^n}$ and $F=\mathbb{F}_{p^d}$, you can recover all the coefficients $s_1,\dots,s_{n/d}$ of the characteristic polynomial of $g$ over $F$ from the first $\phi(n)/d$ of them for all $g$ in the subgroup of $L^*$ of order $\Phi_n(p)$ and not in any proper subfield.

We show that this is in fact false. In particular, when $n=30$, it is false; for $p=7$, $d=1$, no $10$ symmetric polynomials determine all of them, and no $8$ determine any of the others (except the ones determined by the symmetry of the characteristic polynomial). For $p=7$, $d=2$, no $4$ symmetric polynomials determine all of them.

Fact. The order $\Phi_n(p)$ subgroup of $\mathbb{F}_{p^n}^*$ is

$$\{\alpha \in \mathbb{F}_{p^n}^*:N_{\mathbb{F}_{p^n}/M}(\alpha)=1$$    for all $M \subsetneq \mathbb{F}_{p^n}$$$\}.$$

Let $L/k$ be an abelian degree $n$ extension of fields. Let

$$T_{L/k}=\ker\left({\mathrm{Res}}_{L/k}(\mathbb{G}_m) \xrightarrow... ...igoplus_{k \subset M \subsetneq L} {\mathrm{Res}}_{M/k}(\mathbb{G}_m) \right);$$

recall that $\mathbb{G}_m(k)=k^*$, and $({\mathrm{Res}}_{L/k} \mathbb{G}_m)(k)=L^*$. If $L/k$ is not cyclic, $\dim(T_{L/k})=0$. If $L/k$ is cyclic, then $T_{L/k}$ is an algebraic torus over $k$ of dimension $\phi(n)$, i.e. $T_{L/k}$ is isomorphic over $\overline{k}$ to $\mathbb{G}_m^{\phi(n)}$. Here, $T_{L/k} \cong_{L} \mathbb{G}_m^{\phi(n)}$.

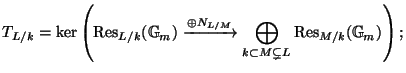
Assume from now on that $L/k$ is cyclic. Then

$$T_{L/k}(k)=\{\alpha \in L^*:N_{L/M}(\alpha)=1$$ for all $k \subset M \subsetneq L$$$\}.$$

Conjecture. [Voskresenskii] $T_{L/k}$ is rational, i.e. there exists a birational map $T_{L/k} \to \mathbb{A}^{\phi(n)}$.

This is true if $n=p^a$ or $p^aq^b$ (Klyachko 1988). It is not known for $n=pqr$. Let us look at the case when $n=2$, say, ${\mathrm{char}}k \neq 2$. Then $L=k(\sqrt{d})$, and $T_{L/k}=\ker(N_{L/k})$ which is a conic which can be parameterized, and we obtain

$$\psi:\mathbb{P}^1 \xrightarrow{\sim} T_{L/k}$$

$$a \mapsto (a+\sqrt{d})/(a-\sqrt{d})$$

$$\infty \mapsto 1$$

We have $\psi(a)\psi(b)=\psi((ab+d)/(a+b))$. (This is also just Hilbert's theorem 90.) Writing $T_n$ for $T_{L/k}$ when $k=\mathbb{F}_q$, this induces a way to do the multiplication in $T_2$ in $\mathbb{P}^1(k)$.

We also give an explicit example when $n=6$ for ${\mathrm{char}}(k) \neq 3$, $[k(\zeta_9):k]=6$ (e.g. $k=\mathbb{F}_q$ with $q \equiv 2,5 \pmod{9}$). $T_{L/k}$ is dimension 2 and contained in ${\mathrm{Res}}_{M/k}(T_{L/M})=T' \sim_k \mathbb{A}^3$ where $M/k$ is the subextension of degree 3. But $T_{L/M}=\ker(N_{L/M})$ is dimension 1, and $N_{L/F}=1$ defines a hypersurface in $T' \sim \mathbb{A}^3$. Therefore $T_6 \sim \mathbb{A}_2$, so we can use the multiplication in $T_6$ but represent elements of $T_6$ by 2 elements of $\mathbb{F}_8$. This gives rise to the cryptosystem CEILIDH.

Open problems:

1. Improve the efficiency of multiplication and exponentiation for the system CEILIDH.
2. Repeat this analysis for $n=30$, i.e.
   1. Find explicit birational isomorphisms between $T_{30}$ and $\mathbb{A}^8$,
   2. Find prime powers $q$ of size $1024/30 \approx 35$ bits such that $\Phi_{30}(q)$ has a $160$-bit prime factor,
   3. Are there special attacks on DL in $\mathbb{F}_{q^{30}}^*$?

Now we look to understand LUC, XTR, and Beyond in terms of algebraic tori. For $H$ a subgroup of ${\mathrm{Gal}}(L/k)=G$ which is a direct factor, write $\Sigma_H$ for the group of permutations of $H$. Then $\Sigma_H$ acts on

$$\textstyle{\bigoplus}_{\sigma \in G} \mathbb{A}^1 \xrightarrow{\s... ... {\mathrm{Res}}_{L/k} \mathbb{A}^1 \supset {\mathrm{Res}}_{L/k}(\mathbb{G}_m).$$

Let

$$X_F={\mathrm{img}}\left(T_{L/k} \to {\mathrm{Res}}_{L/k}(\mathbb{G}_m)/\Sigma_{{\mathrm{Gal}}(L/F)}\right).$$

For LUC and XTR, you look at

$$\{{\mathrm{Tr}}_{L/F}(\alpha):\alpha \in T_{L/k}(k)\}$$

which is the image of $T_{L/k}(k)$ under $T_{L/k} \to X_F \to {\mathrm{Res}}_{F/k}(\mathbb{A}^1)$, where the latter map is a birational isomorphism.

$$\xymatrix @R=0.5in@C=0.7in{ T_{L/k} \ar@{-»}[d] \ar[drr]^{{\math... ...{{\mathrm{Tr}}_{L/F}} & {\mathrm{Res}}_{F/k}(\mathbb{A}^1) \ar[r]^{\sim} & F }$$

Assume that $n$ is squarefree. Write ${\mathrm{Gal}}(L/F)=H_1 \times \dots \times H_t$ where $H_i$ are cyclic of prime order.

Theorem. The action of $\Sigma_{H_i}$ on ${\mathrm{Res}}_{L/k}(\mathbb{G}_m)$ preserves $T_{L/k}$ and $X_F$ is birational to $T_{L/k}/(\Sigma_{H_1} \times \dots \times \Sigma_{H_t})$.

In XTR, we obtain $X_F$ birational to $T_6/S_3$; in the cases $n=30$ and $d=1,2$, one gets $T_{30}/(S_2 \times S_3 \times S_5)$, $T_{30}/(S_3 \times S_5)$, which are not groups.

We have maps $L \to F$ for every symmetric function $s_1,\dots,s_{[L:F]}$. We have a surjection $T_{L/k} \to X_F$ and an injection $X_F \hookrightarrow F^{[L:F]}$ by the direct sum of these functions. A BHV conjecture implies that for the subset consisting of the first $\lceil \phi(n)/d \rceil$ functions (where $d=[F:k]$), the map remains injective. Further, a BHF conjecture implies that every $n$ has a divisor $d$ so that $d$ also divides $\phi(n)$, and the map $X_F \to \mathbb{A}^{\phi(n)}$ (induced by the first $\phi(n)/d$ symmetric functions) is a birational isomorphism. This is true for $(n,d)=(1,1)$ (DH), $(2,1)$ (LUC), $(6,2)$ (XTR), and $(\ell,1)$ and $(2\ell,2)$ where $\ell$ is prime (see Doing more with fewer bits, by Brouwer-Pellikaan-Verheul), but:

Theorem. This is false for $n=30$ ($d=1,2$) if ${\mathrm{char}}(k)$ lies outside a finite set.

To prove this, we first do a computer search for $2$ elements of $T_{30}(\mathbb{F}_7)$ with the same image $a \in (\mathbb{F}_7)^8$ but different images in $X_F$. Using Hensel's Lemma, every lift of $a$ to $\mathbb{Z}_7^8$ has at least 2 inverse images in $X_F(\mathbb{Q}_7)$. Therefore the map is not generically one-to-one over $\mathbb{Q}_7$, so it is not generically one-to-one over $\mathbb{Q}$, hence over any field of characteristic 0. Then reduce modulo $p$ to get it over $\mathbb{F}_p$ and therefore all fields of characteristic $p$ (outside of a finite set).

Back to the main index for Future directions in algorithmic number theory.