Let ![]() be a smooth, geometrically integral variety over
be a smooth, geometrically integral variety over ![]() (a number
field), and suppose that
(a number
field), and suppose that ![]() is projective. We denote by
is projective. We denote by
![]() the closure of
the closure of ![]() in
in
![]() .
.
Here our aim is to: (i) explain the counterexamples to weak approximation;
(ii) find `intermediate' sets ![]() between
between
![]() and
and
![]() ;
(iii) in some cases, prove that
;
(iii) in some cases, prove that
![]() .
.
General setting
Let ![]() be an algebraic group (usually linear, but not necessarily connected,
e.g.
be an algebraic group (usually linear, but not necessarily connected,
e.g. ![]() finite). If
finite). If ![]() is commutative:
define
is commutative:
define ![]() the étale cohomology groups (
the étale cohomology groups (![]() ; the cohomological
dimension of a number field forgetting real places makes the higher
cohomology groups uninteresting). In general, we have only the pointed set
; the cohomological
dimension of a number field forgetting real places makes the higher
cohomology groups uninteresting). In general, we have only the pointed set
![]() (defined by Cech cocycles for the étale topology). If
(defined by Cech cocycles for the étale topology). If
![]() ,
,
![]() , where
, where
![]() . If
. If ![]() is linear,
is linear, ![]() corresponds to
corresponds to ![]() -torsors over
-torsors over ![]() up to isomorphism.
up to isomorphism.
Take
![]() , define
, define
Obviously
![]() . We will see that in many cases
. We will see that in many cases
![]()
Example.
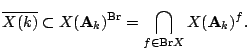
(Indeed the Brauer group of the ring of integers of ![]() is zero).
is zero).
![]() is the Brauer-Manin set of
is the Brauer-Manin set of ![]() . Manin showed
in 1970 that for a genus one curve with finite Tate-Shafarevich group,
the condition
. Manin showed
in 1970 that for a genus one curve with finite Tate-Shafarevich group,
the condition
![]() implies the existence
of a rational point.
implies the existence
of a rational point.
Remark.
If ![]() is rational, then
is rational, then
![]() is finite,
where
is finite,
where
![]() . Then
. Then
![]() is
`computable'.
is
`computable'.
Theorem. [H, Skorobogatov]
If ![]() is linear and
is linear and
![]() , then
, then
![]() (and
(and
![]() is "computable").
is "computable").
Abelian descent theory
This was developed by Colliot-Thélène and Sansuc, and recently completed by Skorobogatov.
Theorem. Define
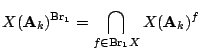
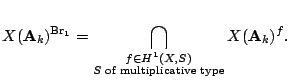
This Theorem is difficult, see Skorobogatov's book for a complete account
on the subject. One of the ideas is to recover the Brauer group of ![]() (mod.
(mod.
![]() ) making
cup-products
) making
cup-products
![]() , where
, where
![]() and
and
![]() is the class of
is the class of ![]() in
in
![]() .
.
Now assume that ![]() is a rational variety, so
is a rational variety, so
![]() (since
(since
![]() ). Assume
). Assume
![]() . Consider a universal torsor
. Consider a universal torsor
![]() . If
. If
![]() , can define
, can define
![]() where
where
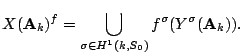
If you can prove that the torsors ![]() satisfy weak approximation,
then
satisfy weak approximation,
then
![]() , so the Brauer-Manin
obstruction is the only one.
, so the Brauer-Manin
obstruction is the only one.
Example. There are many examples of this:
If ![]() is reducible, we can have a counterexample to weak approximation, e.g.
is reducible, we can have a counterexample to weak approximation, e.g.
![]() , where
, where
![]() ,
,
![]() , in
some cases there is an obstruction given by the Hilbert symbol
, in
some cases there is an obstruction given by the Hilbert symbol ![]() .
.
Theorem. [Sansuc 1981]
Let ![]() be a linear connected algebraic group over
be a linear connected algebraic group over ![]() ,
, ![]() a smooth
compactification of
a smooth
compactification of ![]() , then the Brauer-Manin obstruction is the only one:
, then the Brauer-Manin obstruction is the only one:
Back to fibration methods
If ![]() is a fibration, we saw that if the base and the fibres
satisfy weak approximation, under certain circumstances then
is a fibration, we saw that if the base and the fibres
satisfy weak approximation, under certain circumstances then ![]() satisfies
weak approximation.
satisfies
weak approximation.
Here we consider
![]() , a projective, surjective morphism (and
the generic fibre
, a projective, surjective morphism (and
the generic fibre ![]() is smooth). Assume also that all fibres are
geometrically integral (can do with all but one because of strong
approximation on the affine line).
is smooth). Assume also that all fibres are
geometrically integral (can do with all but one because of strong
approximation on the affine line).
![]()
Theorem. [H 1993, 1996]
Yes,
![]() if you assume that:
if you assume that:
Two ideas:
Applications: (i) Recover Sansuc's result just knowing the case of a torus;
(ii) If you know that
![]() for
for ![]() a smooth
cubic surface, then by induction the same holds for hypersurfaces, so if
a smooth
cubic surface, then by induction the same holds for hypersurfaces, so if
![]() , then
, then ![]() satisfies weak approximation.
satisfies weak approximation.
Nonabelian descent
If ![]() is a finite but not commutative
is a finite but not commutative ![]() -group, it is possible that for
-group, it is possible that for
![]() ,
,
![]() .
.
Theorem. [Skorobogatov 1997]
There exists
![]() a bi-elliptic surface such that
a bi-elliptic surface such that
![]() ,
,
![]() .
.
Actually:
![]() for some
for some
![]() ,
,
![]() .
.
There are similar statements for weak approximation (H 1998), e.g.
take ![]() any
bi-elliptic surface,
any
bi-elliptic surface,
![]() , then
, then
![]() .
.
Nevertheless the Brauer-Manin condition is quite strong, as shows the following result :
Theorem. [H 2001] We have:
Open question : is the first part of this theorem still true for
a ![]() which is an extension of a finite abelian group by a connected
linear group ? My guess is "no".
which is an extension of a finite abelian group by a connected
linear group ? My guess is "no".
Back to the
main index
for Rational and integral points on higher dimensional varieties.