Mazur: Families of rationally connected subvarieties


Introduction

This is joint work with Graber, Harris, and Starr.

Throughout, we let $ k$ be any finite field and $ K$ a field of transcendence degree $ 1$ over $ \mathbb{C}$. We have two classical results, due to Chevalley-Warning and Tsen, for $ k$ and $ K$, respectively: a hypersurface of low degree has a rational point; a hypersurface of low degree $ X$ is one with $ \deg X \leq \dim X+1$.

Inspired by these theorems, one (i.e. Artin) defines a field $ F$ to be quasi-algebraically closed if every hypersurface of low degree over $ F$ has a $ F$-rational point. In view of resent results due to Kollár, Kollár-Miyaoka-Mori, and Graber-Harris-Starr, we ask similar questions not for hypersurfaces but for certain other classes of varieties.

We generalize the notion of hypersurfaces of low degree to rationally connected varieties over $ \mathbb{C}$ which are projective and smooth: a variety $ X$ is rationally connected if for any two points $ p,q \in X$, there exists a rational curve $ C \subset X$ with $ p,q \in C$. Rationally connected varieties are closed under birational transformation, products, domination (if $ X \to Y$ is dominant, and $ X$ is rationally connected, then $ Y$ is rationally connected), and specialization. This is a much better class of varieties than, say, rational varieties (consider the difficulty in determining which cubic $ 4$-folds are rational).

There is another candidate for a generalization of hypersurfaces of low degree: a variety $ X$ over $ F$ is $ \mathscr{O}$-acyclic if

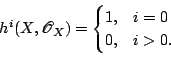
\begin{displaymath} h^i(X,\mathscr{O}_X)= \begin{cases} 1, & i=0 \\ 0, & i>0. \end{cases} \end{displaymath}

Rationally connected varieties are $ \mathscr{O}$-acyclic.

The only rationally connected curves are rational curves; the only rationally connected surfaces are rational surfaces. However, there are $ \mathscr{O}$-acyclic surfaces which are not rational, e.g. Enriques surfaces.

Theorem. If $ X$ is a smooth hypersurface over $ \mathbb{C}$, then it is equivalent for $ X$ to be of low degree, rationally connected, and $ \mathscr{O}$-acyclic.

Theorem. [Generalized Chevalley-Warning; Katz] Any $ \mathscr{O}$-acyclic variety over $ k$ has a $ k$-rational point.

Over $ \mathbb{C}$, and given an endomorphism $ f:X \to X$, one defines the Lefschetz number $ L(f)=\sum (-1)^i {\mathrm{tr}}(F\vert H^i)$; this complex number measures the fixed point locus of $ f$. Over a finite field, the Lefschetz number counts the number of fixed points, at least modulo $ p$; one computes that the Lefschetz number is $ 1 \bmod p$.

For the generalization to rationally connected varieties over $ K$, a variety $ X$ over $ K$ can be thought of as a family of rationally connected varieties over a curve $ X \to C$. By family we always mean that although the base $ C$ might not be proper or smooth, the morphism is proper and generically smooth.

Theorem. [Generalized Tsen; Graber, Harris, Starr] Any rationally connected variety over $ K$ has a $ K$-rational point.


A converse

Given a family $ X \to B$, a section is a triangle

$\displaystyle \xymatrix{ B \ar[r] \ar[dr]^{=} & X \ar[d] \\ & B. }$

We define a pseudo-section to be a triangle

$\displaystyle \xymatrix{ S \ar[r] \ar[dr] & X \ar[d] \\ & B; }$

where $ S \to B$ is a family of rationally connected varieties. Since a point is rationally connected, a section gives a pseudo-section.

We can rephrase the GHS theorem in this language as follows: If $ f:X \to B$ is a family with a pseudo-section, then its restriction $ f_C:X_C \to C$ to every smooth curve $ C \hookrightarrow B$ has a section.

Theorem. [Weak converse to GHB] If $ f:X \to B$ is a family such that every restriction $ f_C:X_C \to C$ for every smooth curve $ C \hookrightarrow B$ has a section, then $ f:X \to B$ has a pseudo-section.

This theorem is related to Lefschetz's theorem about $ \pi_1$ as can be seen by restricting attention to finite étale covers.


Applications

This theorem has application to finding varieties $ X/K$ with no rational point; in particular:

Corollary. There exists an Enriques surface over some $ K$ with no $ K$-rational point.

This is completely ineffective; an open question is to find the genus of the curve given by this counterexample.


\begin{ques} Is there an Enriques surface over $\mathbb{Q}(t)$\ with no rational point over $\mathbb{C}(t)$? \end{ques}

Every Enriques surfaces over $ k$ has a point over $ k$; this is not the case over $ K$, so we have distinguished finite fields from function fields of transcendence degree $ 1$ over $ \mathbb{C}$. We ask: in the Artin-Lang philosophy, what kinds of varieties are cut out by $ \mathscr{O}$-acyclic varieties?

We have another corollary:

Corollary. A family of curves of genus $ 1$ over a base $ B$ has a section if and only if it has a section over every curve $ C \subset B$.

The corollary is clear: a family of curves of genus $ 1$ has no room for a pseudo-section.


Number Theoretic Applications

Now we consider $ \pi:X \to B$ a family defined over a number field; we say $ \pi$ is arithmetically surjective if and only if $ X(L) \to B(L)$ is surjective for all finite extensions $ L/F$.

If $ X \to B$ is a family of curves of genus $ \geq 1$, is it the case that arithmetic surjectivity is equivalent to the existence of a section over $ F$? This question is unapproachable in full generality.

Instead, let us take a very small fragment of it: let $ B$ be a nonempty open subset of $ \mathbb{P}^1$ over $ F=\mathbb{Q}$, $ X \to B$ a family of genus $ 1$ curves, we say it belongs to its Jacobian $ E \to B$. We consider quadratic twist elliptic pencils; given any $ E_1/\mathbb{Q}:y^2=g(x)$, we have the pencil $ E_t/\mathbb{Q}:ty^2=g(x)$. We have the problem: For all $ X \to B$ belonging to $ E_t$, is is true that arithmetic surjectivity holds if and only if a section exists? Work of Skinner-Ono can be used to establish this for all elliptic curves $ E_1/\mathbb{Q}$.



Back to the main index for Rational and integral points on higher dimensional varieties.