List of open problems
Problem/Question 1.
Consider hypersurfaces
![$ f_d \in \mathbb{Z}[x_0,\dots,x_n]$](img1.gif) of degree
of degree 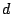 in
in
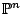 ,
, 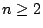 . Let
. Let
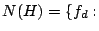
max coefficient of
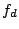
is
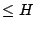
,
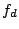
has a solution in
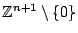
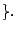
- For
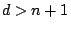 , is it true that
, is it true that
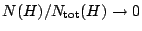 ? Does this follow from Lang's conjectures? (Voloch)
? Does this follow from Lang's conjectures? (Voloch)
- Instead, look at those with those with points locally everywhere
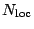 (Poonen). Is this a positive fraction, i.e. is
(Poonen). Is this a positive fraction, i.e. is
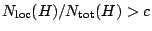 ?
?
- As a special case, if you write down a plane cubic, how likely is it to have a rational point? (Voloch)
- For cubic surfaces, there are examples where the Hasse principle fails, but maybe for almost all values of a parameter in a family, the Hasse principle holds. We should have asympotically that the
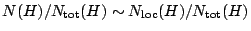 ? (Colliot-Thélène) For
? (Colliot-Thélène) For 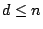 , we hope this will hold in general.
, we hope this will hold in general.
Remarks.
- The set of reducible such hypersurfaces are a very small fraction (usually codimension
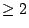 )--they affect this calculation very little (Poonen).
)--they affect this calculation very little (Poonen).
- Serre looked at
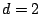 ; here one has the Hasse principle. (Tschinkel) For
; here one has the Hasse principle. (Tschinkel) For 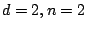 , the proportion of everywhere locally solvable ones tends to zero; but we should exclude this case because of the codimension
, the proportion of everywhere locally solvable ones tends to zero; but we should exclude this case because of the codimension 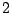 condition. (Heath-Brown) Instead, we should restrict to families
condition. (Heath-Brown) Instead, we should restrict to families 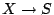 such that the codimension of reducible fibers is at
such that the codimension of reducible fibers is at 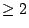 .
.
- Computational evidence is all over the place, so one must rephrase the question better to get some kind of answer. For example, for cubics, those with prime power discriminant and the general evidence are quite different. (Swinnerton-Dyer)
- How is this related to
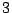 -torsion elements in
-torsion elements in
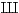 ? (Ellenberg)
? (Ellenberg)
Update (4/21/04): [Poonen and Volloch have tackled this problem:]
Problem/Question 2.
If  is smooth projective geometrically rationally connected defined over a number field
is smooth projective geometrically rationally connected defined over a number field  , then the Brauer-Manin obstruction should be the only one to the Hasse principle. That is, is
, then the Brauer-Manin obstruction should be the only one to the Hasse principle. That is, is
As special cases, this should be the case for Fano varieties of dimension 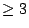 , e.g. (smooth) complete intersections of degree
, e.g. (smooth) complete intersections of degree
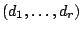 in
in
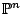 with
with
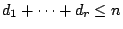 . (Colliot-Thélène)
. (Colliot-Thélène)
Remarks.
- It would be worth doing a reasonably large search on diagonal quartic
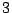 -folds. (Swinnerton-Dyer)
-folds. (Swinnerton-Dyer)
- It is an old problem that for nonsingular cubic forms in at least
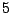 variables, the Hasse principle holds. For diagonal cubic forms over
variables, the Hasse principle holds. For diagonal cubic forms over
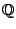 , this is proved modulo finiteness of
, this is proved modulo finiteness of
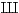 . (Swinnerton-Dyer)
. (Swinnerton-Dyer)
- For the smooth intersection of two quadrics in
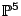 , the Hasse principle should hold? If it has a rational point, then it in fact satisfies weak approximation. The critical problem is in
, the Hasse principle should hold? If it has a rational point, then it in fact satisfies weak approximation. The critical problem is in 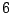 variables. (Colliot-Thélène)
variables. (Colliot-Thélène)
Problem/Question 3.
Let
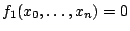 ,
,
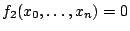 define the smooth complete intersection of two quadrics
define the smooth complete intersection of two quadrics
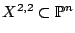 over
over 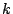 a number field. For simplicity, assume
a number field. For simplicity, assume
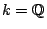 .
If
.
If 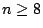 ,
,
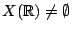 implies
implies
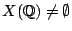 . (Sansuc, Swinnerton-Dyer, Colliot-Thélène)
. (Sansuc, Swinnerton-Dyer, Colliot-Thélène)
- For
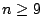 (
(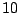 variables), this can be provably done by the circle method. (Heath-Brown)
variables), this can be provably done by the circle method. (Heath-Brown)
- For
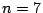 , there is the concrete problem: given two quadratic forms
, there is the concrete problem: given two quadratic forms 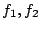 as above in
as above in 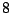 variables over
variables over 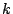 a
a 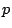 -adic field, assume
-adic field, assume 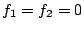 is smooth, so that
is smooth, so that
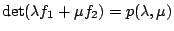 is separable. Does there exist
is separable. Does there exist
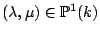 such that
such that
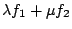 contains 3 hyperbolics (split off an extra
contains 3 hyperbolics (split off an extra 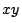 in its decomposition). Solution to this problem would give a local-global principle for
in its decomposition). Solution to this problem would give a local-global principle for 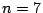 . (Colliot-Thélène)
. (Colliot-Thélène)
Remarks.
- It is possible in odd characteristic after an odd degree field extension (Heath-Brown), unwritten.
- If in the pencil, there is one of rank
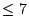 , then it is possible; or other conditions with
, then it is possible; or other conditions with 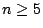 (e.g. two conjugate lines or contains a conic defined over the ground field).
(e.g. two conjugate lines or contains a conic defined over the ground field).
Problem/Question 4.
Consider the hypersurface given by
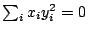 in
in
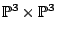 . Take the height
. Take the height
and throw out the set where some 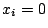 ,
, 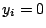 . Can one estimate the counting function? (Peyre)
. Can one estimate the counting function? (Peyre)
Remarks.
Some people are working on this. What news?
Problem/Question 5.
Consider
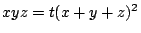 , with height function
, with height function
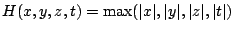 , and restrict to
, and restrict to
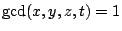 . Excluding trivial solutions (on lines), can you prove a counting function which is
. Excluding trivial solutions (on lines), can you prove a counting function which is
This is a singular cubic surface so we also expect an explicit constant. (Tschinkel)
Remarks.
- This has a
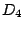 -singular point. On top of the singularity, one gets a configuration of 4 lines all of which have self-intersection
-singular point. On top of the singularity, one gets a configuration of 4 lines all of which have self-intersection 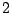 .
.
- Are numerics possible? (Voloch)
- This is a compactification of the affine plane (solve for
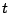 ), but it is not equivariantly embedded. (Tschinkel)
), but it is not equivariantly embedded. (Tschinkel)
- For the singular cubic surface
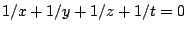 , Heath-Brown
has established that the counting function has exact order of
magnitude
, Heath-Brown
has established that the counting function has exact order of
magnitude
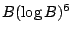 .
Proceedings of the session in analytic number theory and Diophantine
equations, Bonner Math. Schriften 360 (2003).
.
Proceedings of the session in analytic number theory and Diophantine
equations, Bonner Math. Schriften 360 (2003).
- Progress: Using the universal torsor (as calculated by Hassett and
Tschinkel) Browning has established that the counting function has exact
order of magnitude
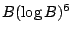 .
See math.AG/0403530,
[http://front.math.ucdavis.edu/math.NT/0404245].
.
See math.AG/0403530,
[http://front.math.ucdavis.edu/math.NT/0404245].
- Update (4/21/04) Tim Browning has shown
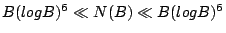 . He makes use of the universal torsor. See
[
arXiv:math.NT/0404245]
. He makes use of the universal torsor. See
[
arXiv:math.NT/0404245]
- Takloo-Bighash: for
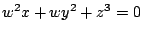 , have an effective
lower bound of
, have an effective
lower bound of 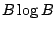 , and should be able to get
, and should be able to get
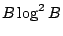 by a similar method, but can't push it any further. Expected
upper bound in this case is again
by a similar method, but can't push it any further. Expected
upper bound in this case is again
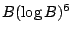 .
Hassett: the universal torsor was in his lecture.
.
Hassett: the universal torsor was in his lecture.
- Hassett: there are 13(ish) singular cubics (zero-dimensional in
moduli), the list is in a paper, reference available.
Problem/Question 6.
(Swinnerton-Dyer)
- Is there a
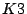 surface
surface  over
over
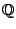 which has a finite nonzero number of rational points
which has a finite nonzero number of rational points
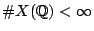 ?
?
- Is there a nonsingular quartic surface
 with this property?
with this property?
- Find a third rational point on
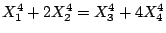 . (There are only 2 points with height
. (There are only 2 points with height
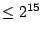 , and other non-public reasons to believe that there are only finitely many points.)
, and other non-public reasons to believe that there are only finitely many points.)
- Find a smooth quartic
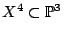 with
with
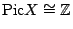 and
and 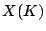 infinite.
infinite.
Remarks.
- Over
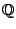 would be the first place to try, but over any number field is OK. It seems as though this is possible for either all such families or no such family.
would be the first place to try, but over any number field is OK. It seems as though this is possible for either all such families or no such family.
- There are
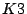 surfaces with no rational lines with infinitely many rational points. (Peyre)
surfaces with no rational lines with infinitely many rational points. (Peyre)
- Do you hope that the Brauer-Manin obstruction is the only one to weak approximation? (Harari)
- The rank of the Neron-Severi group over
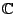 is rank
is rank 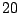 , but is only rank
, but is only rank 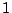 over
over
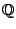 coming from the hyperplane section. Therefore it looks like a Kummer surface, the product of two CM elliptic curves. What are the elliptic curves? (Read the right paper of Shioda.) The CM is by
coming from the hyperplane section. Therefore it looks like a Kummer surface, the product of two CM elliptic curves. What are the elliptic curves? (Read the right paper of Shioda.) The CM is by
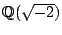 ?
?
- It does not seem helpful to look over a finite extension. (Colliot-Thélène)
- Are there any heuristics looking modulo any primes? (Poonen) The zeta function does not say anything about solubility. (Swinnerton-Dyer)
- On
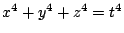 , Elkies found another point, with smallest height on the order of
, Elkies found another point, with smallest height on the order of 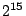 (Colliot-Thélène); he uses a fibered pencil of elliptic curves, looks at values of the parameter for which there was a point everywhere locally and then looked for a global point. There is no such fibration in this case. Maybe one could go to an extension and then look for rational points (Villegas).
(Colliot-Thélène); he uses a fibered pencil of elliptic curves, looks at values of the parameter for which there was a point everywhere locally and then looked for a global point. There is no such fibration in this case. Maybe one could go to an extension and then look for rational points (Villegas).
- What restrictions are necessary for such a surface to occur? (Poonen) The condition to ensure that
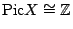 is a black-board full. (Swinnerton-Dyer)
is a black-board full. (Swinnerton-Dyer)
- Is it possible for the given surface that
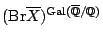 is finite? If so, there might be many rational points. (Harari) In the computations of Brauer-Manin obstructions, there are many with
is finite? If so, there might be many rational points. (Harari) In the computations of Brauer-Manin obstructions, there are many with
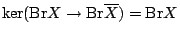 , there are a lack of examples with `transcendental elements'. We expect
, there are a lack of examples with `transcendental elements'. We expect
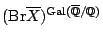 to be finite, proven in certain cases because of the Tate conjecture.
to be finite, proven in certain cases because of the Tate conjecture.
- Are there any known examples of quartic surfaces with
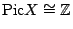 with infinitely many rational points? (Poonen) Maybe almost always they have infinitely many. (Swinnerton-Dyer)
with infinitely many rational points? (Poonen) Maybe almost always they have infinitely many. (Swinnerton-Dyer)
- If there are infinitely many points on a quartic, will they be Zariski dense? Look in Mordell's book, perhaps. (Colliot-Thélène)
- Silverman has examples of surfaces in
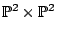 with two noncommuting endomorphisms, so this gives infinitely many points, but this has Picard group rank 2. (Voloch)
with two noncommuting endomorphisms, so this gives infinitely many points, but this has Picard group rank 2. (Voloch)
Problem/Question 7.
The distribution of rational points on Enriques surfaces has not been
well studied. (Skorobogatov)
Let  be an Enriques surface.
be an Enriques surface.
- If
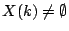 , is
, is 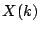 Zariski dense?
Zariski dense?
- Is there an
 which violates the Hasse principle?
which violates the Hasse principle?
- Is there an
 such that
such that
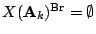 but
but
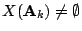 ?
?
- Is there an
 with
with
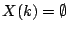 ,
,
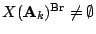 ?
?
Remark.
There is a
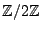 cover of the Enriques surface
cover of the Enriques surface  which is a
which is a
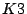 surface; is there some torsor over the
surface; is there some torsor over the 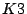 surface for the torus
for which the total space is a torsor for
surface for the torus
for which the total space is a torsor for  under a nonabelian
group? For a bi-elliptic surface, is this possible? (Harari)
under a nonabelian
group? For a bi-elliptic surface, is this possible? (Harari)
Problem/Question 8.
Let  an Enriques surface over a number field
an Enriques surface over a number field 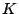 ,
,
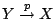 the double cover (K3 surface),
the double cover (K3 surface),
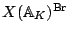 the Brauer-Manin set.
Take
the Brauer-Manin set.
Take
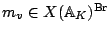 , lift it to an adelic point
, lift it to an adelic point
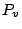 on
on 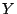 . Under what assumptions on
. Under what assumptions on 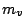 will it be liftable
to
will it be liftable
to 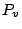 on
on
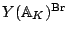 , or at least
, or at least
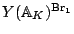 ?
?
Remark.
Guess (reported by Harari): there should be some nonabelian torsor
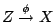 for the group
for the group 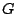 which is the semidirect
product
which is the semidirect
product
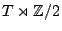 , where
, where 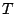 is Neron-Severi torus of
is Neron-Severi torus of 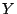 .
The points
.
The points
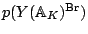 should correspond to
should correspond to
 ,
where
,
where
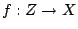 .
.
Remark.
About Pb/question 8 (which is closely related to Pb 7), David Harari
adds the following update (2004-09-25): ``Skorobogatov and myself have
recently proved that there exist Enriques surfaces  with adelic
points in
with adelic
points in
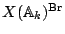 but not in the closure of the set of
rational points
but not in the closure of the set of
rational points 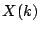 ("The Manin obstruction to weak approximation
is not the only one"). In particular, some adelic points of
("The Manin obstruction to weak approximation
is not the only one"). In particular, some adelic points of
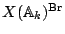 are not liftable to
are not liftable to
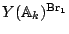 , see the
paper "Non-abelian descent and the arithmetic of Enriques surfaces"
at
[http://www.dma.ens.fr/~{}harari/].''
, see the
paper "Non-abelian descent and the arithmetic of Enriques surfaces"
at
[http://www.dma.ens.fr/~{}harari/].''
Problem/Question 9.
Use the intermediate Jacobian (when it is an abelian variety) in arithmetic? To fix ideas, 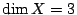 , look at algebraic
, look at algebraic 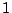 -cycles modulo rational equivalence.
-cycles modulo rational equivalence.
Compute this for a rigid Calabi-Yau 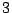 -fold
-fold  (over
(over
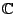 ), i.e.
), i.e.
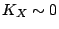 ,
,  simply connected,
simply connected, 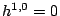 ,
, 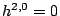 ,
, 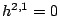 ,
, 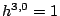 . In this case, the intermediate Jacobian
. In this case, the intermediate Jacobian
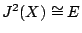 is of dimension
is of dimension 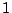 . Determine
. Determine 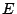 given
given  , i.e. give its
, i.e. give its 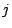 -invariant.
-invariant.
Remarks.
- For two quadratic forms
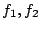 in
in 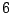 variables, i.e.
variables, i.e.
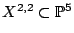 , look at the Jacobian of the genus
, look at the Jacobian of the genus 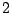 curve given by
curve given by
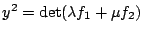 . (Colliot-Thélène) Over
. (Colliot-Thélène) Over
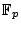 , you can prove the Weil conjecture for
, you can prove the Weil conjecture for 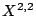 . Can you use this to prove something? You can also look at the variety of lines on
. Can you use this to prove something? You can also look at the variety of lines on 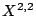 , also a principal homogeneous space for an abelian variety; so over a finite field, this will have a rational point, so there will be a line over
, also a principal homogeneous space for an abelian variety; so over a finite field, this will have a rational point, so there will be a line over
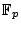 . We can say something with
. We can say something with 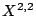 contains a pair of skew conjugate lines or a conic defined over the ground field; how can you do these things such as finding a line over a quadratic field...?
contains a pair of skew conjugate lines or a conic defined over the ground field; how can you do these things such as finding a line over a quadratic field...?
- Explicit examples of rigid Calabi-Yau
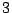 -folds? Take an elliptic curve
-folds? Take an elliptic curve 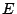 with complex multiplication by
with complex multiplication by
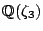 , take the kernel of the endomorphism
, take the kernel of the endomorphism 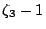 ,
, 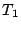 ;
;
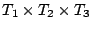 has
has 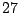 singular points, blowing up these points gives
singular points, blowing up these points gives 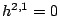 (Candela). Also the quintic hypersurface
(Candela). Also the quintic hypersurface
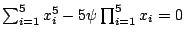 with
with 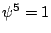 has
has 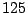 nodes; the resolution has
nodes; the resolution has 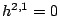 . There are more such examples. (Yui)
. There are more such examples. (Yui)
Problem/Question 10.
Are there results at the level of number fields arising from the techniques of rationally connected varieties? (Colliot-Thélène)
For example, recently Kollàr got nice results over local fields: if 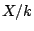 is a projective variety, we say
is a projective variety, we say
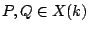 are
are 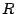 -equivalent if you can link them by a chain of curves of genus zero over
-equivalent if you can link them by a chain of curves of genus zero over 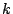 ; if
; if  is smooth with
is smooth with
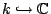 , then
, then  is rationally connected if
is rationally connected if
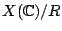 is a single point. Kollar proved that if
is a single point. Kollar proved that if 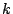 is a local field, and
is a local field, and 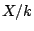 is rationally connected, then
is rationally connected, then 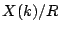 is finite. (Szobó)
is finite. (Szobó)
Kollàr and Szabo proved that if 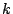 is a number field, and
is a number field, and 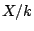 is rationally connected, then
is rationally connected, then 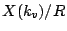 is trivial for almost all
is trivial for almost all 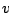 .
.
Remark.
If 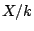 is a variety over a number field, and
is a variety over a number field, and  is rationally connected, then does there exist a field
is rationally connected, then does there exist a field
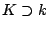 such that for all
such that for all
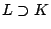 that
that 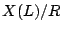 consists of a point? (Ellenberg) Negative answer by a conic bundle over
consists of a point? (Ellenberg) Negative answer by a conic bundle over
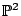 . (Raskind)
. (Raskind)
Problem/Question 11.
Let 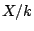 be a smooth projective rationally connected variety with the cohomological dimension of
be a smooth projective rationally connected variety with the cohomological dimension of 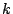
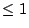 . Does
. Does  have a rational point? (Colliot-Thélène)
have a rational point? (Colliot-Thélène)
Remarks.
- There was a false proof for
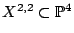 .
.
- Yes if
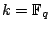 . (Esnault) Yes if
. (Esnault) Yes if 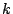 is the function field of a curve. (Harris, Graber, Starr)
is the function field of a curve. (Harris, Graber, Starr)
- At least for surfaces, we hoped that universal torsors would be nice objects, e.g. they are birational to homogeneous spaces under a nice group, so they would be close to
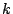 -rational if they had a
-rational if they had a 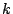 -point. An example of
-point. An example of 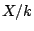 (
(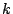 a horrible field) a cubic surface with
a horrible field) a cubic surface with
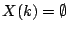 but
but
![$ ({\mathrm{Br}}k)[3]=0$](img147.gif) . (Madore, Colliot-Thélène)
. (Madore, Colliot-Thélène)
- Colliot-Thélène adds the following:
With hindsight, Problem 11, as phrased, had been settled by J. Ax in
Bull. Am. Math. Soc. 71 (1965) p. 717. Ax
produced a smooth hypersurface in 9-dimensional
projective space, of degree 5, over a field
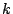 of cohomological dimension 1, with no rational
point (that such hypersurfaces are rationally
connected was proven much later).
Ax'example has index 1, i.e. the g.c.d. of the degree of the finite
field extensions over which the hypersurface acquires a rational point is 1.
In Journal of the Inst. of Math. Jussieu (2004) 3 p. 1-16,
J.-L. Colliot-Thélène and D. Madore produce a
field of cohomological dimension 1
and a smooth cubic surface over that field which has index 3, thus settling
negatively a question of Kato and Kuzumaki (1986).
of cohomological dimension 1, with no rational
point (that such hypersurfaces are rationally
connected was proven much later).
Ax'example has index 1, i.e. the g.c.d. of the degree of the finite
field extensions over which the hypersurface acquires a rational point is 1.
In Journal of the Inst. of Math. Jussieu (2004) 3 p. 1-16,
J.-L. Colliot-Thélène and D. Madore produce a
field of cohomological dimension 1
and a smooth cubic surface over that field which has index 3, thus settling
negatively a question of Kato and Kuzumaki (1986).
Problem/Question 12.
Describe all pairs of sets
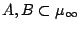 ,
,
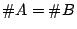 , stable under
, stable under
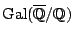 , where the elements of
, where the elements of 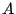 and
and 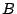 are alternately placed around the unit circle. (Rodriguez-Villegas)
are alternately placed around the unit circle. (Rodriguez-Villegas)
Remarks.
- There is a solution but it is much more complicated than the statement of the problem. The solution is used in the classification of algebraic hypergeometric functions.
- There is the infinite family
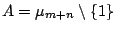 and
and
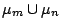 with
with
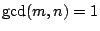 .
.
Problem/Question 13.
Find a smooth quintic hypersurface in
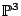 with Picard number 1 over
with Picard number 1 over
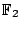 . (Voloch)
. (Voloch)
Remarks.
- This is used in constructing error correcting codes.
- If you compute the analytic rank (the zeta function), by Tate's theorem, the second Betti number is
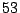 so compute the number of points up to something like
so compute the number of points up to something like
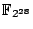 (Voloch). So testing them exhaustively would be very costly.
(Voloch). So testing them exhaustively would be very costly.
- Shioda has examples over
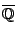 of Picard number
of Picard number 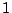 , so they might be defined over
, so they might be defined over
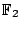 . (Raskind) This has been tried once. (Voloch)
. (Raskind) This has been tried once. (Voloch)
Problem/Question 14.
Consider cubic hypersurfaces
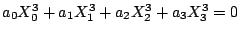 . (Swinnerton-Dyer)
. (Swinnerton-Dyer)
- If soluble, give upper bound for smallest solution in terms of the
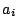 .
.
- Look at
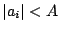 , tabulate the size of the smallest solution and conjecture a particular growth rate in terms of
, tabulate the size of the smallest solution and conjecture a particular growth rate in terms of 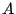 .
.
Remarks.
If
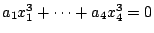 has a solution
has a solution
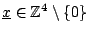 , how large is the smallest solution?
Let
, how large is the smallest solution?
Let
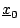 be a solution with
be a solution with
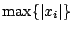 minimal.
Swinnerton-Dyer had suggested: if
minimal.
Swinnerton-Dyer had suggested: if
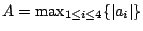 ,
then
,
then
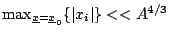 .
Wooley had suggested instead
.
Wooley had suggested instead
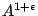 .
.
Progress: Stoll, Stein:
computations up to
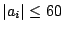 suggest an upper bound of
suggest an upper bound of
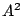 . Also, assuming Schinzel, finiteness of Sha, and one unproven lemma,
Stoll can produce
. Also, assuming Schinzel, finiteness of Sha, and one unproven lemma,
Stoll can produce
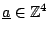 with least solution
with least solution
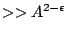 . (Need the hypotheses to ensure that the examples
do have rational solutions.)
. (Need the hypotheses to ensure that the examples
do have rational solutions.)
Shape of examples: if 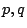 prime, look at
prime, look at
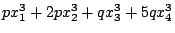 . Assume
. Assume 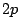 and
and 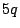 are approximately of the same
size,
are approximately of the same
size,
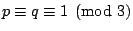 , that
, that 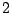 is a cube mod
is a cube mod 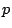 but not mod
but not mod
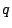 , and that 5 is a cube mod
, and that 5 is a cube mod 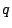 but not mod
but not mod 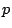 (plus some additional
technical conditions).
(plus some additional
technical conditions).
Remarks.
- The growth rate should be like
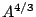 . If you do the corresponding thing with
. If you do the corresponding thing with 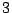 squares,
squares,
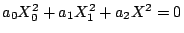 , the answer is
, the answer is 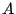 . (Swinnerton-Dyer)
. (Swinnerton-Dyer)
- Seems more like
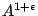 . (Wooley)
. (Wooley)
- Is there a heuristic which suggests this? (Poonen) No. (Swinnerton-Dyer)
Problem/Question 15.
Characterize the rational numbers 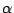 that can be written as
that can be written as
for
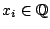 and fixed
and fixed 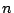 . (Poonen)
. (Poonen)
It is necessary that
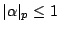 for
for 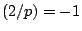 and
and 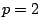 . Is it sufficient?
. Is it sufficient?
Remarks.
- You might repeat this kind of problem with any rational function with no rational poles. (As in Waring's problem.) Something has already been done for a function with rational poles. (Poonen)
- You can phrase this problem a different kind of way: prove or disprove the Hasse principle for this equation for all
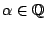 . (Swinnerton-Dyer) You can probably show for
. (Swinnerton-Dyer) You can probably show for 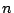 sufficiently large (and fixed) that there is a solution locally.
sufficiently large (and fixed) that there is a solution locally.
- There are applications to Diophantine definitions: this would show that inside
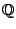 , the set of these rational numbers which are integral at half of the places, is Diophantine. (Poonen)
, the set of these rational numbers which are integral at half of the places, is Diophantine. (Poonen)
Problem/Question 16.
Solve the local-global solubility problem for finding lines on a cubic hypersurface. (Wooley)
- Find an example of a cubic hypersurface over
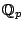 (in as many variables as possible) with no rational line.
(in as many variables as possible) with no rational line.
- Find an example of a cubic hypersurface over
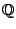 (in as many variables as possible) with no rational line.
(in as many variables as possible) with no rational line.
Remarks.
- For (a), we must have at least
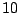 variables, since there are cubic forms in
variables, since there are cubic forms in 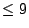 variables with no point. If you have
variables with no point. If you have 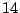 variables, then there is a rational line. (Wooley)
variables, then there is a rational line. (Wooley)
- For (b), for
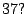 variables, there is a rational line. (Wooley)
variables, there is a rational line. (Wooley)
- Also, find one with a rational point but no rational line. (Colliot-Thélène)
Problem/Question 17.
Draw a regular pentagon 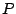 , construct the circle through the
, construct the circle through the 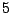 vertices
vertices 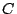 , and consider the curve
, and consider the curve
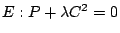 . This is a quintic curve with
. This is a quintic curve with 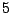 double points, and therefore has geometric genus
double points, and therefore has geometric genus 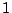 . This curve has five points at
. This curve has five points at 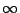 (given by the slopes of the lines). Compute the
(given by the slopes of the lines). Compute the 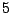 -torsion of
-torsion of 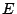 . (McCallum)
. (McCallum)
Remarks.
- The points at
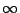 are among the
are among the 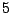 -torsion.
-torsion.
- The motivation is: these curves are principal homogeneous spaces, and are candidates for
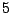 -torsion elements in
-torsion elements in
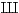 . If
. If 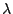 is the parameter on
is the parameter on 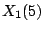 , then this is a twist of the universal elliptic curve of
, then this is a twist of the universal elliptic curve of 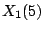 . Here we have explicit models. (McCallum)
. Here we have explicit models. (McCallum)
- If you consider this as a pencil of elliptic curves, how does this relate to the talks at this conference? (Ellenberg)
- Does the pentagon have to be regular? (Voloch) There are various variations, such as replacing the circle with a star pentagon.
Problem/Question 18.
- Find a separable polynomial
![$ g(t) \in \mathbb{Q}[t]$](img201.gif) such that the Jacobian of the hyperelliptic curve
such that the Jacobian of the hyperelliptic curve 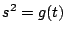 is isogeneous over
is isogeneous over
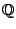 to
to
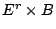 ,
, 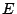 an elliptic curve, with
an elliptic curve, with 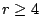 or
or 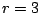 and
and
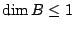 . (Silverberg)
. (Silverberg)
- Related problem: Give an example of a map
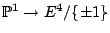 , where
, where 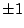 acts diagonally, whose image does not lie in
acts diagonally, whose image does not lie in
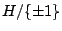 for any subgroup
for any subgroup
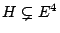 . (Ellenberg)
. (Ellenberg)
Remarks.
- The case
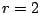 and
and 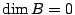 is possible, as is the case
is possible, as is the case 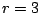 and
and 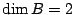 . A consequence of this construction would be better bounds on the density of quadratic twists of
. A consequence of this construction would be better bounds on the density of quadratic twists of 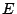 of rank
of rank 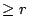 . (Silverberg)
. (Silverberg)
- What if you ask this question over
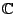 ? (Voloch) Can at least do
? (Voloch) Can at least do 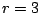 and
and 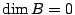 over
over
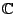 . (Poonen) Even over
. (Poonen) Even over
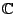 , maybe it cannot be done for large
, maybe it cannot be done for large 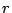 . (Ellenberg)
. (Ellenberg)
- One might consider the curve
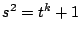 over
over
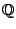 , for
, for 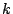 composite. If
composite. If 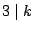 , for example, it maps to
, for example, it maps to 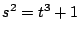 ?
?
- Does it have to be hyperelliptic? (Rodriguez-Villegas) Yes, for applications. (Ellenberg)
- The random matrix heuristics suggest that there is a positive power, so there should be a curve there, and finding such a curve would give a proof of a density result. (Ellenberg)
- Take
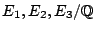 pairwise isogeneous elliptic curves,
pairwise isogeneous elliptic curves,
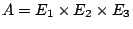 , and look at the set of principal polarizations on
, and look at the set of principal polarizations on  . Find a nonsplit principal polarization on
. Find a nonsplit principal polarization on 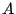 ; then it comes from
; then it comes from
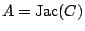 ,
, 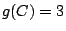 . Now you just need to show that
. Now you just need to show that 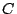 is hyperelliptic.
is hyperelliptic.
Problem/Question 19.
Let  be a variety over a number field
be a variety over a number field 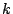 and suppose that for every open Zariski dense
and suppose that for every open Zariski dense
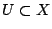 , the map
, the map
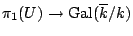 has a splitting
has a splitting 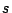 (e.g. if
(e.g. if 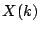 is Zariski dense). In this case, if
is Zariski dense). In this case, if
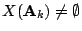 , is there no Brauer-Manin obstruction to the Hasse principle for
, is there no Brauer-Manin obstruction to the Hasse principle for  , i.e. is
, i.e. is
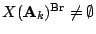 ? (Ellenberg)
? (Ellenberg)
Remarks.
- Is it possible that
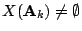 follows from the splitting condition? (Poonen)
You might also ask the corresponding question for a local field. (McCallum)
follows from the splitting condition? (Poonen)
You might also ask the corresponding question for a local field. (McCallum)
- You might also ask this question for other obstructions. (Ellenberg)
Problem/Question 20.
Let
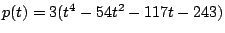 . Write the system of two equations
. Write the system of two equations
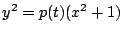 ,
,
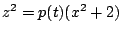 ; think of this as a one-parameter family
; think of this as a one-parameter family  of curves of genus one;
of curves of genus one;
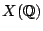 is empty and
is empty and
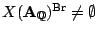 (Skorobogatov).
(Skorobogatov).
Is
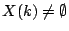 for some
for some
![$ [k:\mathbb{Q}]$](img231.gif) odd? (Colliot-Thélène)
odd? (Colliot-Thélène)
Remarks.
- The secret reason for asking: then
 has a zero-cycle of degree
has a zero-cycle of degree 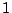 . (Colliot-Thélène)
If you have a zero cycle of degree
. (Colliot-Thélène)
If you have a zero cycle of degree 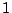 , then there is such a point.
, then there is such a point.
- Even in a given number field of degree
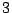 , looking at a random way, the evidence you will find is zero. (Colliot-Thélène)
, looking at a random way, the evidence you will find is zero. (Colliot-Thélène)
- What about
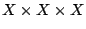 modulo the action by three? (Ellenberg)
modulo the action by three? (Ellenberg)
- Reduce the search by finding one elliptic curve with many rational points (fix
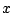 , consider
, consider
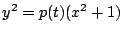 ), then search for
), then search for 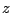 . (Voloch) But the ratio
. (Voloch) But the ratio 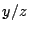 is only dependent on
is only dependent on 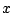 . (Poonen)
. (Poonen)
- Do we expect
![$ [k:\mathbb{Q}]=3$](img236.gif) ? (McCallum) Not necessarily. (Colliot-Thélène)
? (McCallum) Not necessarily. (Colliot-Thélène)
- Consider instead
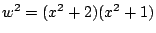 and
and
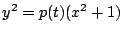 ; search now in the first curve for a cubic point, and search for
; search now in the first curve for a cubic point, and search for 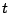 . (Poonen) Put the first one in Weierstrass form, and generate the cubic fields.
. (Poonen) Put the first one in Weierstrass form, and generate the cubic fields.
Problem/Question 21.
Let
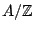 be an algebra with
be an algebra with
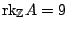 given by its multiplication table. Suppose you know that
given by its multiplication table. Suppose you know that
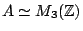 ; find an algorithm which gives an explicit isomorphism. (Stoll)
; find an algorithm which gives an explicit isomorphism. (Stoll)
Remarks.
- The motivation comes from very explicit
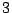 -descent on elliptic curves.
-descent on elliptic curves.
- The case of
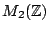 reduces to finding rational points on conics. (Stoll)
reduces to finding rational points on conics. (Stoll)
- Is this an
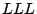 problem? (Voloch) In some sense, but one needs nine
problem? (Voloch) In some sense, but one needs nine
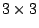 -matrices, not one
-matrices, not one
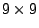 -matrix; the equations are not all linear. (Stoll)
-matrix; the equations are not all linear. (Stoll)
Problem/Question 22.
Let 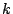 be a number field,
be a number field,
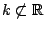 . Construct an algebraic set
. Construct an algebraic set
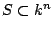 for some
for some 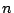 such that the projection onto one of the coordinates is exactly the set of elements of
such that the projection onto one of the coordinates is exactly the set of elements of 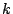 with
with
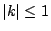 for some (archimedean) absolute value
for some (archimedean) absolute value 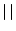 of
of 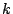 . (Shlapentokh)
. (Shlapentokh)
Remark.
This would imply results on Hilbert's tenth problem for rings of integers. It probably is hard because it is close to being equivalent.
Problem/Question 23.
Let
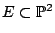 be an elliptic curve over
be an elliptic curve over
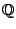 , and suppose
, and suppose
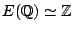 . (Poonen)
. (Poonen)
- Describe
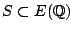 where
where
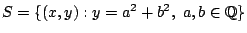 . Is
. Is 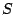 is finite?
is finite?
- More generally,
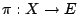 gives a subset
gives a subset
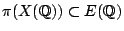 ; what others can you build?
; what others can you build?
Remark.
It is possible to describe in a Diophantine way the set of points
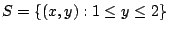 ; this is an infinite set. (Poonen)
; this is an infinite set. (Poonen)
Problem/Question 24.
Given an elliptic curve
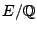 ,
,
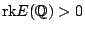 , describe the set of primes
, describe the set of primes 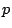 such that
such that
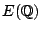 is dense in
is dense in
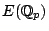 . Is this set nonempty? Is there a modular interpretation of this problem? (Takloo-Bighash)
. Is this set nonempty? Is there a modular interpretation of this problem? (Takloo-Bighash)
Remarks.
- You need surjectivity of the reduction map (Murty and Gupta have some results) and the surjectivity of the map on formal groups (Silverman). One suspects that for any such curve
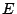 there exists a prime
there exists a prime 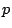 with this property.
with this property.
- This is related to Brauer-type problems for surfaces.
- You should be able to collect data on this to see if there is a positive density. (McCallum)
Problem/Question 25.
Is there an algorithm to decide solubility of a system of linear equations
for
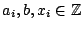 , together with equations of the form
for
, together with equations of the form
for
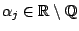 ,
,
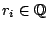 ? (Poonen)
? (Poonen)
Remarks.
- This is a problem in linear programming; add variables. (Voloch)
- A negative answer would have implied undecidability for Hilbert's tenth problem over
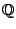 .
.
Problem/Question 26.
Describe the variety of curves of low degree on the Fermat variety
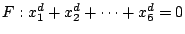 . (Heath-Brown)
. (Heath-Brown)
Remarks.
- Lines are known, but that is all. Hope that there are none or very few.
- The curves should be over
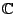 (for now).
(for now).
Problem/Question 27.
Given a plane curve of degree 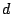 , the number of points on
, the number of points on  of
height at most
of
height at most 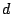 is
is 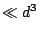 . There are curves which have the
number of rational points
. There are curves which have the
number of rational points 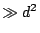 . Can you do better than
. Can you do better than 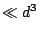 ?
(Heath-Brown)
?
(Heath-Brown)
Remarks.
(Roger Heath-Brown, 2004-09-25) observes that actually 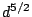 is
easy, so the challenge should be to improve on this.
is
easy, so the challenge should be to improve on this.
Problem/Question 28.
Let 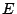 be an elliptic curve over
be an elliptic curve over
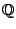 , and
, and
![$ P \in E(\mathbb{Q})[3]$](img270.gif) ,
, 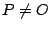 , such that
, such that
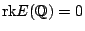 . Let
. Let
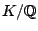 be a cyclic
extension of degree
be a cyclic
extension of degree 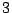 of conductor
of conductor 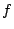 , and let
, and let
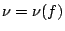 be the
number of distinct primes dividing
be the
number of distinct primes dividing 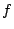 . It is true that
. It is true that
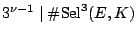 ? (Chantal David)
? (Chantal David)
Remarks.
Let
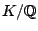 be a cyclic cubic extension. Then the
be a cyclic cubic extension. Then the 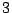 -rank of the
class group of
-rank of the
class group of 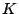 is
controlled by primes dividing discriminant of
is
controlled by primes dividing discriminant of 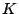 ; if there are
; if there are 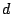 such primes, then
such primes, then 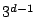 divides the class number
divides the class number
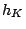 (genus theory). Problem:
carry this over to a guaranteed contribution of 3-primary component
of the 3-Selmer group (over
(genus theory). Problem:
carry this over to a guaranteed contribution of 3-primary component
of the 3-Selmer group (over 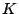 ) of an elliptic curve
) of an elliptic curve
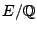 .
Does
.
Does 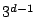 divide the Selmer order?
divide the Selmer order?
Progress: Fix
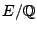 with a rational 3-torsion point, and let
with a rational 3-torsion point, and let 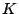 vary as above. Then there is a constant
vary as above. Then there is a constant 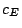 depending only on
depending only on 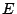 such that
such that 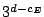 divides the Selmer order.
(Clarification request: do the mean the algebraic part of the
divides the Selmer order.
(Clarification request: do the mean the algebraic part of the 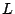 -function,
or the 3-part of the Selmer group, or the group obtained from a 3-descent?
That affects the value of
-function,
or the 3-part of the Selmer group, or the group obtained from a 3-descent?
That affects the value of 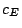 .)
.)
This has been checked computationally (by checking special values of
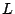 -series).
-series).
Other problems? Poonen: replace 3 by another prime 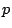 , or replace
, or replace
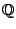 by another number field, etc.
by another number field, etc.
Problem/Question 29.
If 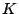 is a field such that all
is a field such that all
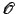 -acyclic varieties over
-acyclic varieties over 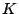 have a point, is
have a point, is
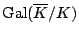 topologically generated by one element?
topologically generated by one element?
Problem/Question 31.
Harmonic analysis and nonabelian torsors:
Takloo-Bighash: Do these give you methods to find rational points?
Hassett: Is there a harmonic analysis argument to count points
on the quintic del Pezzo surface? Wooley: no examples known where
you can combine harmonic analysis with torsors.
Problem/Question 32.
(Voloch):
Given a family of hypersurfaces, show that ``almost all'' members
of the family satisfy the Hasse Principle in ``interesting''
circumstances.
Colliot-Thélène: maybe the opposite?
Poonen: the family was all hypersurfaces of degree 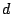 in
in
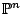 with coefficients of height
with coefficients of height 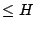 , over some fixed number field
, over some fixed number field 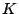 .
The problem was: find the proportion of these that satisfy the
Hasse Principle (originally, that have rational points, but we
can find the local points easily).
.
The problem was: find the proportion of these that satisfy the
Hasse Principle (originally, that have rational points, but we
can find the local points easily).
Wooley and Venkatesh (tentative):
is asymptotic to the product of local densities, at least for
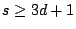 . This is progress for
. This is progress for 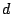 large: for an
individual
large: for an
individual
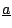 , one has HP (using current technology)
for
, one has HP (using current technology)
for
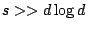 . Proof uses (of course) circle method.
. Proof uses (of course) circle method.
de Jong: for cubics in
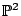 ,
what do conclusions of this type say about 3-Selmer groups of elliptic curves?
,
what do conclusions of this type say about 3-Selmer groups of elliptic curves?
Stoll: given local points, proportion that have rational points (i.e.,
satisfy HP) should be 0.
Mazur: can you put an exponent on that?
Stoll: wait for experimental
evidence.
Problem/Question 33.
(Poonen)
Instead of counting points of bounded height on a variety,
count points of bounded height in a Diophantine set. (I.e.,
counting points in a base the fibre above which has a rational point.)
What
rates of growth can you get? Example: conic bundle over an elliptic
curve. Heuristically, it appears rate of growth can be
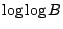 ,
whereas for varieties it always turns out to be
,
whereas for varieties it always turns out to be
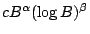 .
.
Problem/Question 34.
(Bogomolov)
Replace Heath-Brown by Arakelov (et al).
with
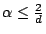 ,
,
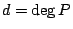 . Analogue for
surfaces, etc.
. Analogue for
surfaces, etc.
Problem/Question 35.
Weak approximation for complex function fields:
Weak approximation over a finite extension 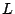 of
of
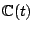 ,
from Hassett's lecture.
,
from Hassett's lecture.
Colliot-Thélène: Known for  a connected linear algebraic group
over
a connected linear algebraic group
over 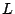 (reduce to reductive groups immediately; since field has
cohomological dimension 1, one has Borel subgroup, reduce to tori;
reduce to quasi-trivial tori, which are open subsets of affine space).
(reduce to reductive groups immediately; since field has
cohomological dimension 1, one has Borel subgroup, reduce to tori;
reduce to quasi-trivial tori, which are open subsets of affine space).
CT: 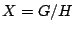 , where
, where 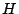 is a subgroup of
is a subgroup of 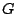 (not necessarily
normal). Same should go through if
(not necessarily
normal). Same should go through if 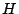 is connected (techniques of
Borovoi et al.).
is connected (techniques of
Borovoi et al.).
CT: Question: Decide whether weak approximation holds for
GL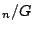 ,
where
,
where 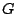 is a finite subgroup of
GL
is a finite subgroup of
GL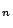 . This seems nontrivial. (de
Jong thinks he can do this; Graber is unsure.) CT says de Jong claims:
Let
. This seems nontrivial. (de
Jong thinks he can do this; Graber is unsure.) CT says de Jong claims:
Let 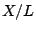 be an arbitrary smooth projective, geometrically and rationally
connected variety. Then weak approxmation holds. (de Jong: do this by
reducing to characteristic
be an arbitrary smooth projective, geometrically and rationally
connected variety. Then weak approxmation holds. (de Jong: do this by
reducing to characteristic 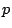 . Not in the dJ-H-S paper.)
. Not in the dJ-H-S paper.)
CT: there is an Enriques surface over
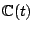 that has a rational
point but does not satisfy weak approximation.
that has a rational
point but does not satisfy weak approximation.
Remarks.
Yuri Tschinkel remarks that there is progress on Nr 35 due to
Colliot-Thelene/Gille and Madore.
To this Brendan Hasset adds that
Madore has announced a proof of weak approximation
in smooth fibers for a cubic surface over the function field
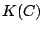 , where
, where 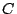 is a curve and
is a curve and 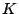 is algebraically closed of
characteristic zero.
is algebraically closed of
characteristic zero.
Back to the
main index
for Rational and integral points on higher dimensional varieties.
![]() of degree
of degree ![]() in
in
![]() ,
, ![]() . Let
. Let
![]() is smooth projective geometrically rationally connected defined over a number field
is smooth projective geometrically rationally connected defined over a number field ![]() , then the Brauer-Manin obstruction should be the only one to the Hasse principle. That is, is
, then the Brauer-Manin obstruction should be the only one to the Hasse principle. That is, is
![]() , e.g. (smooth) complete intersections of degree
, e.g. (smooth) complete intersections of degree
![]() in
in
![]() with
with
![]() . (Colliot-Thélène)
. (Colliot-Thélène)
![]() ,
,
![]() define the smooth complete intersection of two quadrics
define the smooth complete intersection of two quadrics
![]() over
over ![]() a number field. For simplicity, assume
a number field. For simplicity, assume
![]() .
If
.
If ![]() ,
,
![]() implies
implies
![]() . (Sansuc, Swinnerton-Dyer, Colliot-Thélène)
. (Sansuc, Swinnerton-Dyer, Colliot-Thélène)
![]() in
in
![]() . Take the height
. Take the height
![]() , with height function
, with height function
![]() , and restrict to
, and restrict to
![]() . Excluding trivial solutions (on lines), can you prove a counting function which is
. Excluding trivial solutions (on lines), can you prove a counting function which is
![]() be an Enriques surface.
be an Enriques surface.
![]() cover of the Enriques surface
cover of the Enriques surface ![]() which is a
which is a
![]() surface; is there some torsor over the
surface; is there some torsor over the ![]() surface for the torus
for which the total space is a torsor for
surface for the torus
for which the total space is a torsor for ![]() under a nonabelian
group? For a bi-elliptic surface, is this possible? (Harari)
under a nonabelian
group? For a bi-elliptic surface, is this possible? (Harari)
![]() an Enriques surface over a number field
an Enriques surface over a number field ![]() ,
,
![]() the double cover (K3 surface),
the double cover (K3 surface),
![]() the Brauer-Manin set.
Take
the Brauer-Manin set.
Take
![]() , lift it to an adelic point
, lift it to an adelic point
![]() on
on ![]() . Under what assumptions on
. Under what assumptions on ![]() will it be liftable
to
will it be liftable
to ![]() on
on
![]() , or at least
, or at least
![]() ?
?
![]() for the group
for the group ![]() which is the semidirect
product
which is the semidirect
product
![]() , where
, where ![]() is Neron-Severi torus of
is Neron-Severi torus of ![]() .
The points
.
The points
![]() should correspond to
should correspond to
![]() ,
where
,
where
![]() .
.
![]() with adelic
points in
with adelic
points in
![]() but not in the closure of the set of
rational points
but not in the closure of the set of
rational points ![]() ("The Manin obstruction to weak approximation
is not the only one"). In particular, some adelic points of
("The Manin obstruction to weak approximation
is not the only one"). In particular, some adelic points of
![]() are not liftable to
are not liftable to
![]() , see the
paper "Non-abelian descent and the arithmetic of Enriques surfaces"
at
[http://www.dma.ens.fr/~{}harari/].''
, see the
paper "Non-abelian descent and the arithmetic of Enriques surfaces"
at
[http://www.dma.ens.fr/~{}harari/].''
![]() , look at algebraic
, look at algebraic ![]() -cycles modulo rational equivalence.
-cycles modulo rational equivalence.
![]() -fold
-fold ![]() (over
(over
![]() ), i.e.
), i.e.
![]() ,
, ![]() simply connected,
simply connected, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . In this case, the intermediate Jacobian
. In this case, the intermediate Jacobian
![]() is of dimension
is of dimension ![]() . Determine
. Determine ![]() given
given ![]() , i.e. give its
, i.e. give its ![]() -invariant.
-invariant.
![]() is a projective variety, we say
is a projective variety, we say
![]() are
are ![]() -equivalent if you can link them by a chain of curves of genus zero over
-equivalent if you can link them by a chain of curves of genus zero over ![]() ; if
; if ![]() is smooth with
is smooth with
![]() , then
, then ![]() is rationally connected if
is rationally connected if
![]() is a single point. Kollar proved that if
is a single point. Kollar proved that if ![]() is a local field, and
is a local field, and ![]() is rationally connected, then
is rationally connected, then ![]() is finite. (Szobó)
is finite. (Szobó)
![]() is a number field, and
is a number field, and ![]() is rationally connected, then
is rationally connected, then ![]() is trivial for almost all
is trivial for almost all ![]() .
.
![]() is a variety over a number field, and
is a variety over a number field, and ![]() is rationally connected, then does there exist a field
is rationally connected, then does there exist a field
![]() such that for all
such that for all
![]() that
that ![]() consists of a point? (Ellenberg) Negative answer by a conic bundle over
consists of a point? (Ellenberg) Negative answer by a conic bundle over
![]() . (Raskind)
. (Raskind)
![]() be a smooth projective rationally connected variety with the cohomological dimension of
be a smooth projective rationally connected variety with the cohomological dimension of ![]()
![]() . Does
. Does ![]() have a rational point? (Colliot-Thélène)
have a rational point? (Colliot-Thélène)
![]() ,
,
![]() , stable under
, stable under
![]() , where the elements of
, where the elements of ![]() and
and ![]() are alternately placed around the unit circle. (Rodriguez-Villegas)
are alternately placed around the unit circle. (Rodriguez-Villegas)
![]() with Picard number 1 over
with Picard number 1 over
![]() . (Voloch)
. (Voloch)
![]() . (Swinnerton-Dyer)
. (Swinnerton-Dyer)
![]() has a solution
has a solution
![]() , how large is the smallest solution?
Let
, how large is the smallest solution?
Let
![]() be a solution with
be a solution with
![]() minimal.
Swinnerton-Dyer had suggested: if
minimal.
Swinnerton-Dyer had suggested: if
![]() ,
then
,
then
![]() .
Wooley had suggested instead
.
Wooley had suggested instead
![]() .
.
![]() suggest an upper bound of
suggest an upper bound of
![]() . Also, assuming Schinzel, finiteness of Sha, and one unproven lemma,
Stoll can produce
. Also, assuming Schinzel, finiteness of Sha, and one unproven lemma,
Stoll can produce
![]() with least solution
with least solution
![]() . (Need the hypotheses to ensure that the examples
do have rational solutions.)
. (Need the hypotheses to ensure that the examples
do have rational solutions.)
![]() prime, look at
prime, look at
![]() . Assume
. Assume ![]() and
and ![]() are approximately of the same
size,
are approximately of the same
size,
![]() , that
, that ![]() is a cube mod
is a cube mod ![]() but not mod
but not mod
![]() , and that 5 is a cube mod
, and that 5 is a cube mod ![]() but not mod
but not mod ![]() (plus some additional
technical conditions).
(plus some additional
technical conditions).
![]() that can be written as
that can be written as
![]() for
for ![]() and
and ![]() . Is it sufficient?
. Is it sufficient?
![]() , construct the circle through the
, construct the circle through the ![]() vertices
vertices ![]() , and consider the curve
, and consider the curve
![]() . This is a quintic curve with
. This is a quintic curve with ![]() double points, and therefore has geometric genus
double points, and therefore has geometric genus ![]() . This curve has five points at
. This curve has five points at ![]() (given by the slopes of the lines). Compute the
(given by the slopes of the lines). Compute the ![]() -torsion of
-torsion of ![]() . (McCallum)
. (McCallum)
![]() be a variety over a number field
be a variety over a number field ![]() and suppose that for every open Zariski dense
and suppose that for every open Zariski dense
![]() , the map
, the map
![]() has a splitting
has a splitting ![]() (e.g. if
(e.g. if ![]() is Zariski dense). In this case, if
is Zariski dense). In this case, if
![]() , is there no Brauer-Manin obstruction to the Hasse principle for
, is there no Brauer-Manin obstruction to the Hasse principle for ![]() , i.e. is
, i.e. is
![]() ? (Ellenberg)
? (Ellenberg)
![]() . Write the system of two equations
. Write the system of two equations
![]() ,
,
![]() ; think of this as a one-parameter family
; think of this as a one-parameter family ![]() of curves of genus one;
of curves of genus one;
![]() is empty and
is empty and
![]() (Skorobogatov).
(Skorobogatov).
![]() for some
for some
![]() odd? (Colliot-Thélène)
odd? (Colliot-Thélène)
![]() be an algebra with
be an algebra with
![]() given by its multiplication table. Suppose you know that
given by its multiplication table. Suppose you know that
![]() ; find an algorithm which gives an explicit isomorphism. (Stoll)
; find an algorithm which gives an explicit isomorphism. (Stoll)
![]() be a number field,
be a number field,
![]() . Construct an algebraic set
. Construct an algebraic set
![]() for some
for some ![]() such that the projection onto one of the coordinates is exactly the set of elements of
such that the projection onto one of the coordinates is exactly the set of elements of ![]() with
with
![]() for some (archimedean) absolute value
for some (archimedean) absolute value ![]() of
of ![]() . (Shlapentokh)
. (Shlapentokh)
![]() be an elliptic curve over
be an elliptic curve over
![]() , and suppose
, and suppose
![]() . (Poonen)
. (Poonen)
![]() ; this is an infinite set. (Poonen)
; this is an infinite set. (Poonen)
![]() ,
,
![]() , describe the set of primes
, describe the set of primes ![]() such that
such that
![]() is dense in
is dense in
![]() . Is this set nonempty? Is there a modular interpretation of this problem? (Takloo-Bighash)
. Is this set nonempty? Is there a modular interpretation of this problem? (Takloo-Bighash)
![]() . (Heath-Brown)
. (Heath-Brown)
![]() , the number of points on
, the number of points on ![]() of
height at most
of
height at most ![]() is
is ![]() . There are curves which have the
number of rational points
. There are curves which have the
number of rational points ![]() . Can you do better than
. Can you do better than ![]() ?
(Heath-Brown)
?
(Heath-Brown)
![]() is
easy, so the challenge should be to improve on this.
is
easy, so the challenge should be to improve on this.
![]() be an elliptic curve over
be an elliptic curve over
![]() , and
, and
![]() ,
, ![]() , such that
, such that
![]() . Let
. Let
![]() be a cyclic
extension of degree
be a cyclic
extension of degree ![]() of conductor
of conductor ![]() , and let
, and let
![]() be the
number of distinct primes dividing
be the
number of distinct primes dividing ![]() . It is true that
. It is true that
![]() ? (Chantal David)
? (Chantal David)
![]() be a cyclic cubic extension. Then the
be a cyclic cubic extension. Then the ![]() -rank of the
class group of
-rank of the
class group of ![]() is
controlled by primes dividing discriminant of
is
controlled by primes dividing discriminant of ![]() ; if there are
; if there are ![]() such primes, then
such primes, then ![]() divides the class number
divides the class number
![]() (genus theory). Problem:
carry this over to a guaranteed contribution of 3-primary component
of the 3-Selmer group (over
(genus theory). Problem:
carry this over to a guaranteed contribution of 3-primary component
of the 3-Selmer group (over ![]() ) of an elliptic curve
) of an elliptic curve
![]() .
Does
.
Does ![]() divide the Selmer order?
divide the Selmer order?
![]() with a rational 3-torsion point, and let
with a rational 3-torsion point, and let ![]() vary as above. Then there is a constant
vary as above. Then there is a constant ![]() depending only on
depending only on ![]() such that
such that ![]() divides the Selmer order.
(Clarification request: do the mean the algebraic part of the
divides the Selmer order.
(Clarification request: do the mean the algebraic part of the ![]() -function,
or the 3-part of the Selmer group, or the group obtained from a 3-descent?
That affects the value of
-function,
or the 3-part of the Selmer group, or the group obtained from a 3-descent?
That affects the value of ![]() .)
.)
![]() -series).
-series).
![]() , or replace
, or replace
![]() by another number field, etc.
by another number field, etc.
![]() is a field such that all
is a field such that all
![]() -acyclic varieties over
-acyclic varieties over ![]() have a point, is
have a point, is
![]() topologically generated by one element?
topologically generated by one element?
![]() in
in
![]() with coefficients of height
with coefficients of height ![]() , over some fixed number field
, over some fixed number field ![]() .
The problem was: find the proportion of these that satisfy the
Hasse Principle (originally, that have rational points, but we
can find the local points easily).
.
The problem was: find the proportion of these that satisfy the
Hasse Principle (originally, that have rational points, but we
can find the local points easily).
![]() ,
what do conclusions of this type say about 3-Selmer groups of elliptic curves?
,
what do conclusions of this type say about 3-Selmer groups of elliptic curves?
![]() ,
whereas for varieties it always turns out to be
,
whereas for varieties it always turns out to be
![]() .
.
![]() of
of
![]() ,
from Hassett's lecture.
,
from Hassett's lecture.
![]() a connected linear algebraic group
over
a connected linear algebraic group
over ![]() (reduce to reductive groups immediately; since field has
cohomological dimension 1, one has Borel subgroup, reduce to tori;
reduce to quasi-trivial tori, which are open subsets of affine space).
(reduce to reductive groups immediately; since field has
cohomological dimension 1, one has Borel subgroup, reduce to tori;
reduce to quasi-trivial tori, which are open subsets of affine space).
![]() , where
, where ![]() is a subgroup of
is a subgroup of ![]() (not necessarily
normal). Same should go through if
(not necessarily
normal). Same should go through if ![]() is connected (techniques of
Borovoi et al.).
is connected (techniques of
Borovoi et al.).
![]() ,
where
,
where ![]() is a finite subgroup of
GL
is a finite subgroup of
GL![]() . This seems nontrivial. (de
Jong thinks he can do this; Graber is unsure.) CT says de Jong claims:
Let
. This seems nontrivial. (de
Jong thinks he can do this; Graber is unsure.) CT says de Jong claims:
Let ![]() be an arbitrary smooth projective, geometrically and rationally
connected variety. Then weak approxmation holds. (de Jong: do this by
reducing to characteristic
be an arbitrary smooth projective, geometrically and rationally
connected variety. Then weak approxmation holds. (de Jong: do this by
reducing to characteristic ![]() . Not in the dJ-H-S paper.)
. Not in the dJ-H-S paper.)
![]() that has a rational
point but does not satisfy weak approximation.
that has a rational
point but does not satisfy weak approximation.
![]() , where
, where ![]() is a curve and
is a curve and ![]() is algebraically closed of
characteristic zero.
is algebraically closed of
characteristic zero.