Colliot-Thelene 1: Rational points on surfaces with a pencil of curves of genus one

Symmetrizing the Computation of the Selmer Group

Let $k$ be a field, ${\mathrm{char}}k = 0$, $E:y^2=(x-e_1)(x-e_2)(x-e_3)$ an elliptic curve with $e_i \in k$ so that all $2$-torsion of $E$ is rational. We have the exact sequence

$$0 \to E[2] \to E \xrightarrow{2} E \to 0$$

where $E[2] \cong (\mathbb{Z}/2\mathbb{Z})^2$. The long exact sequence in Galois cohomology gives

$$0 \to E(k)/2E(k) \to H^1(k,E[2]) \to H^1(k,E)[2] \to 0$$

where $H^1(k,E[2]) \cong (k^*/k^{*2})^2$ classifies $2$-coverings: that is, given $(\alpha_1,\alpha_2) \in (k^*/k^{*2})^2$, we have the $2$-cover defined by the equations: $x-e_1=\alpha_1u_1^2$, $x-e_2=\alpha_2u_2^2$, $x-e_3=(\alpha_1\alpha_2)^{-1}u_3^2$. The group $H^1(k,E)$ classifies principal homogeneous spaces.

Now let $k$ be a number field, $\Omega$ the set of places of $k$. We have the diagram

$$\xymatrix @C=12pt{ & & {\mathrm{Sel}}(E,2) \ar[r] \ar[d] & \text{... ...v) \ar[r] & \prod_v H^1(k_v,E[2]) \ar[r] & \prod_v H^1(k_v,E)[2] \ar[r] & 0 }$$

so ${\mathrm{Sel}}(E,2)$ gives $2$-covers with points everywhere locally, and $^2(k,E)$ measures the difference.

Over a local field, we have a pairing

$$H^1(k_v,E[2]) \times H^1(k_v,E[2]) \to H^2(k_v,\mu_2)$$

induced by the Weil pairing, which is nondegenerate and alternating, so that $(x,x)=0$.

Fact. [Tate] $E(k_v)/2E(k_v) \hookrightarrow H^1(k_v,E[2])$ is maximal isotropic for the above pairing.

If $E/k$ has good reduction at $k_v$, then $E(k_v)/2E(k_v) = E(\mathcal{O}_v)/2E(\mathcal{O}_v) \simeq H^1(\mathcal{O}_v,E[2])$, which is $(\mathcal{O}_v^*/\mathcal{O}_v^{*2})^2 \subset (k_v^*/k_v^{*2})^2$, the maximal isotropic subgroup.

Suppose $S \subset \Omega$ is a finite set of places, and suppose $S$ contains the primes above $\infty,2$, and the primes of bad reduction. Then

$$\xymatrix @C=0pt{ \bigoplus_{v \in S}E(k_v)/2E(k_v) \ar[d] & \tim... ...r[rr]^>>>>>>>>>>{\sum e_v} & \ \ \ \ \ \ \ \ \ \ \ \ & \mathbb{Z}/2\mathbb{Z}}$$

Then ${\mathrm{Sel}}(E,2)$ is the right kernel of $e$.

Fact. If ${\mathrm{Cl}}(\mathcal{O}_S)=0$, then $i$ is injective.

This follows from class field theory. So we choose $S_0$ such that ${\mathrm{Cl}}(\mathcal{O}_{S_0})=0$, and take $S \supset S_0$. If ${\mathrm{Cl}}(\mathcal{O}_S)=0$, $i$ is an injection, and the image of $i$ is a maximal isotropic subgroup of $V_S=\bigoplus_{v \in S}V_v$, $V_v=H^1(k_v,E[2])$.

What we have achieved: the Selmer group ${\mathrm{Sel}}(E,2)$ is now a kernel of `a square matrix', since $\bigoplus_{v \in S}E(k_v)/2E(k_v)$ and $H^1(\mathcal{O}_S,E[2])$ have the same dimension over $\mathbb{F}_2$. Letting $\mathfrak{h}(A)=(A^*/A^{*2})^2$, we have

$$W_S \times \mathfrak{h}(\mathcal{O}_S) \to \mathbb{Z}/2\mathbb{Z}$$

where

$$W_S=\bigoplus_{v \in S} W_v,\ W_v=E(k_v)/2E(k_v).$$

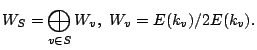
Proposition. Assume $S \supset S_0$ (containing primes above $\infty,2$ and those of bad reduction and such that ${\mathrm{Cl}}(\mathcal{O}_{S_0})=0$) is a finite set of places. Suppose that $\mathfrak{h}(\mathcal{O}_S) \subset V_S$ is a maximal isotropic subgroup. Then there exist $K_v \subset V_v$ for $v \in S$ maximal isotropic such that $K_v=\mathfrak{h}(\mathcal{O}_v)$ for $v \in S \setminus S_0$, and

$$\mathfrak{h}(\mathcal{O}_S) \oplus \bigoplus_{v \in S} K_v=V_S.$$

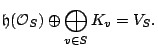
This is purely a result in linear algebra.

Recall we have $W_S \times \mathfrak{h}(\mathcal{O}_S) \to \mathbb{Z}/2\mathbb{Z}$ from $W_S \subset V_S$ and $\mathfrak{h}(\mathcal{O}_S) \subset V_S$.

Definition. We let ${\mathrm{Sel}}(E,2) \subset \mathcal{I}^S \subset \mathfrak{h}(\mathcal{O}_S)$, where

$$\mathcal{I}^S=\{\xi \in \mathfrak{h}(\mathcal{O}_S):$$for all $v \in S$, $\xi \in K_v+W_v$$$\}.$$

We let

$$\mathcal{W}_S=\bigoplus_{v \in S} W_v/(W_v \cap K_v).$$

We then have a pairing

$$\mathcal{W}_S \times \mathcal{I}^S \xrightarrow{e_S} \mathbb{Z}/2\mathbb{Z}.$$

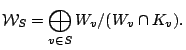
Proposition. The Selmer group is the kernel of $e_S$. The map $\tau:\mathcal{I}^S \simeq \mathcal{W}_S$ is an isomorphism. For $\mu \in \mathcal{I}^S$, we define a map

$$\mu=\textstyle{\sum}_{v \in S} \alpha_v+\beta_v \mapsto \textstyle{\sum}_{v \in S} \alpha_v;$$

via $\tau$, the new pairing $\mathcal{W}_S \times \mathcal{I}^S \to \mathbb{Z}/2\mathbb{Z}$ is symmetric.

Example. For $E:y^2=(x-e_1)(x-e_2)(x-e_3)$, $e_i \in \mathcal{O}_v$, $v(\prod(e_i-e_j))=1$ (reduction is of type $I_2$). Then

$$\xymatrix{ E(k_v)/2E(k_v) \ar@{->}[r] \ar[dr] & (k_v^*/k_v^{*2})^... ...] \ar[u] \ar@{->>}[r] & \mathbb Z/2\mathbb Z\subset (\mathbb Z/2\mathbb Z)^2 }$$

Here $W_v/(W_v \cap K_v)=\mathbb{Z}/2\mathbb{Z}$, $W_v \cong (\mathbb{Z}/2\mathbb{Z})^2$.

Algebraico-Geometric version of Selmer group

Let $k$ be a field, ${\mathrm{char}}k = 0$, $E:y^2=(x-c_1(t))(x-c_2(t))(x-c_3(t))$, so $E$ is defined over $F=k(t)$. To simplify, we assume that all $p_i=c_i-c_j$ are of the same even degree. We also assume that $r(t)=\prod(c_i-c_j)$ is separable, $r(t)=\rho \prod_{M \in \mathcal{M}} r_M(t)$ where $\rho \in k^*$, $r_M$ monic irreducible, so $E$ has reduction type $I_2$.

Now assume $k$ is a totally imaginary number field. The Neron model $\mathcal{E}/\mathbb{P}^1$ has

$$0 \to \mathcal{E}^* \to \mathcal{E}\to \textstyle{\bigoplus}_{M \in \mathcal{M}} i_{M*} \mathbb{Z}/2\mathbb{Z}\to 0.$$

Let $V \subset \mathbb{A}^1={\mathrm{Spec}}k(t)$ be $V=\mathbb{A}^1 \setminus \{r=0\}$.

Let $\mathcal{S}\subset \mathfrak{h}(k(V))$ consist of triples $(m_1,m_2,m_3)$, $m_i \in k(t)$ squarefree, $(\prod_{i=1}^{3} m_i)$ is a square which divides $r(t)^2$, and $\gcd(m_i,p_i)=1$.

Put another way, we have

$$\xymatrix{ 0 \ar[r] & \mathcal{E}(F)/2\mathcal{E}(F) \ar[r] & \ma... ...{E}) \ar[r] \ar[d] & 0 \\ & & (F^*/F^{*2})^2 \ar[r] & H^1(F,E)[2] \ar[r] & 0 }$$

Corresponding to $m=(m_1,m_2,m_3)$, we have the surface $X_m$ defined by the equations $x-e_i(t)=m_i(t)u_i^2$, $i=1,2,3$. Then $X_m/\mathbb{P}^1$ has a minimal model if and only if $X_m/\mathbb{P}^1$ is locally isomorphic for the étale topology with $\mathcal{E}/\mathbb{P}^1$.

We have a map

$$\mathcal{S}\xrightarrow{\delta} \bigoplus_{M \in \mathcal{M}} (k_M^*/k_M^{*2})$$

where $k_M=k[t]/r_M(t)$. We see that $E(F)/2E(F) \subset \ker \delta$.

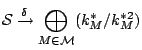
Theorem. [Theorem A] Suppose that $\ker \delta$ is the image of $E(F)[2]$. (In particular, the generic rank is zero.) Assume Schinzel's hypothesis. Then there exist infinitely many $x \in \mathbb{P}^1(k)$ such that ${\mathrm{rk}}E_x(k)=0$.

Theorem. [Theorem B] Let $m \in \mathcal{S}$, and assume that

$$\ker\left(\mathcal{S}\to \bigoplus_M k_M^*/(k_M^{*2},\delta_M(m))\right)=E(F)[2] \oplus \mathbb{Z}/2\mathbb{Z}.$$

Assume Schinzel's hypothesis. Assume $X_m(\mathbf A_k)^{{\mathrm{Br}}_1(X)} \neq \emptyset$. Then there exist infinitely many $x \in \mathbb{P}^1(k)$ such that $E_x(k)$ is of rank one and $X_{m,x}(k) \neq \emptyset$.

Back to the main index for Rational and integral points on higher dimensional varieties.