We had
![]() ,
, ![]() , and
, and
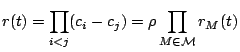
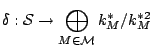
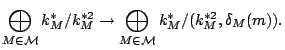
Fact.
![]() .
.
Theorem. [Theorem B]
Assume Schinzel's hypothesis, and the finiteness of
![]() . Let
. Let
![]() ,
,
![]() . Let
. Let
![]() . Assume:
. Assume:
![]() , and
, and
![]() .
.
Then
![]() is infinite, and
is infinite, and ![]() is Zariski dense.
is Zariski dense.
Here,
Schinzel's hypothesis: Let
![]() for
for
![]() be distinct irreducible polynomials with leading coefficient positive (plus technical condition, to exclude polynomials like
be distinct irreducible polynomials with leading coefficient positive (plus technical condition, to exclude polynomials like ![]() ); then there exist infinitely many values
); then there exist infinitely many values
![]() such that each
such that each ![]() is a prime.
is a prime.
Remark.
The assumption that
![]() is satisfied for general
is satisfied for general ![]() . For the assumption that
. For the assumption that
![]() , in general we have
, in general we have
![]() so this reduces to
so this reduces to
![]() .
.
The proof of this theorem will take up the rest of these notes.
We shall define a finite set
![]() of `bad places'. For each
of `bad places'. For each ![]() , we have some
, we have some
![]() , and we look for
, and we look for
![]() , with
, with ![]() very close to
very close to ![]() for
for ![]() , and find one
, and find one ![]() such that:
such that:
We have
![]() , containing
, containing ![]() -adic places and those over
-adic places and those over ![]() (note we are being sloppy for real places), and places of bad reduction of
(note we are being sloppy for real places), and places of bad reduction of
![]() , of
, of
![]() , and such that
, and such that
![]() . If
. If
![]() , then
, then
![]() is separable (finite étale cover).
is separable (finite étale cover).
We look at ![]() and look at its prime decomposition; it will have some part in
and look at its prime decomposition; it will have some part in ![]() and another part
and another part ![]() of primes of multiplicity
of primes of multiplicity ![]() , and one prime
, and one prime ![]() , the `Schinzel prime'. We realize
, the `Schinzel prime'. We realize
![]() for
for ![]() . Then
. Then
![]() has bad reduction in
has bad reduction in
![]() .
.
First we find ![]() such that
such that
![]() . For
. For
![]() , we introduce the algebra
, we introduce the algebra
![]() , where
, where ![]() is the quadratic extension connected to
is the quadratic extension connected to ![]() . Then
. Then
![]() . A priori,
. A priori,
![]() . Since
. Since ![]() is even,
is even,
![]() .
.
Let
![]() , with projection
, with projection
![]() . We know that
. We know that
![]() . For almost all places of
. For almost all places of ![]() ,
,
![]() is trivial.
is trivial.
Fix ![]() as before plus places where some
as before plus places where some ![]() is not trivial on
is not trivial on ![]() . Now
. Now
![]() . Fix
. Fix
![]() for
for ![]() with this property. Note
with this property. Note
![]() . Suppose
. Suppose
![]() is very close to
is very close to ![]() for
for ![]() and the decomposition of
and the decomposition of ![]() has all primes in
has all primes in ![]() split in
split in ![]() .
.
Claim.
For such ![]() ,
,
![]() .
.
For the second part, we now need to control the Selmer groups uniformly in the family
![]() , for
, for ![]() satisfying
satisfying ![]() , namely,
, namely, ![]() is very close to
is very close to ![]() for
for ![]() ,
, ![]() decomposes into primes in
decomposes into primes in ![]() ,
, ![]() primes splitting in
primes splitting in ![]() , and the Schinzel prime
, and the Schinzel prime ![]() .
.
Let
![]() , and
, and
![]() . We have
. We have
![$\displaystyle \xymatrix{
0 \ar[r] & \mathfrak{h}(\mathcal{O}_T) \ar[r] \ar[d] &...
...{ord}}_M} &
\bigoplus_{M \in \mathcal{M}}(\mathbb Z/2\mathbb Z)^2 \ar[r] & 0
}$](img89.gif)
Here
We find two `constant' subgroups ![]() . First, we find
. First, we find
![]() , fixed because
, fixed because ![]() very close to
very close to ![]() for
for ![]() . For the second pair:
. For the second pair:
Proposition. For each
![]() , there exists a unique
, there exists a unique
![]() such that for any
such that for any ![]() with
with ![]() ,
,
![]() , and for each
, and for each ![]() , its component in
, its component in ![]() belongs to
belongs to ![]() .
.
We define the subgroup
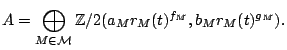
Proposition.
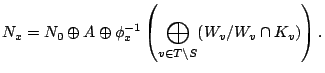
Proposition. On
![]() , the restriction of the pairing
, the restriction of the pairing ![]() is independent of
is independent of ![]() .
.
To prove this, use various reciprocity laws.
To conclude, write
![]() , where
, where
![]() ,
,
![]() , and
, and ![]() is the supplement. Use the assumption that
is the supplement. Use the assumption that
![]() to get rid of
to get rid of ![]() ...
...
Now use finiteness of
![]() and Cassels-Tate pairing,
and Cassels-Tate pairing,
![]()
![]()
![]() implies
implies
![]()
![]() , so the rank is
, so the rank is ![]() .
.
Back to the
main index
for Rational and integral points on higher dimensional varieties.