Recent progress on
Quantum Unique Ergodicity (QUE)
by Peter Sarnak
October 3, 2008
Techniques for studying the fine behaviour of a highly excited state in the quantization of classically chaotic hamiltonian, are limited. The basic general tool is the theory of Fourier Integral Operators and related microlocal analysis and it provides information about averages of various quantities associated with these states. Over the last 25 years, the development of fast numerical methods to compute such states has exposed interesting phenomena and conjectures (the corresponding study is called quantum chaos) but little of the finer structure that is observed, can be proved.
Among the many interesting conjectures that have emerged is one which asks about the distribution in the semiclassical limit of the familiar probability measure ("Wigner measure") on phase space, that is associated with a given quantum state. Any limit of these measures is called a quantum limit. The behaviour in the semiclassical limit of almost all states for the quantization of a classically ergodic hamiltonian mechanical system is one of the few well understood phenomena in the subject. The quantum analogue of ergodicity is the Quantum Ergodicity Theorem (due to Shnirelman, Colin de Verdiere and Zelditch) and it asserts that in the semiclassical limit, almost all these states become equidistributed with respect to the corresponding classical Lioville measure. The Quantum Unique Ergodicity Conjecture (Rudnick and Sarnak) "QUE", asserts that for certain strongly chaotic hamiltonians (specifically geodesic motion on the unit tangent space of a manifold of negative sectional curvature) every state becomes equidistributed. This conjecture which was based on insights from the arithmetic case (see below) was contrary to what was suggested by some numerics, namely that some states may concentrate along unstable periodic orbits (known as strong scars). QUE, if true, is in sharp contrast to the behaviour of the classical trajectories for such chaotic systems. It limits the extent to which the correspondence principle is valid for chaotic systems.
In this generality the main breakthrough on the problem is due to Nalini Anantharaman who has shown that strong scars cannot occur for hamiltonians coming from the geodesic motion on a compact negatively curved manifold. In fact she shows that any quantum limit must have positive entropy. This is remarkable result whose proof combines ideas from micro-local analysis with hyperbolic dynamics in a novel way.
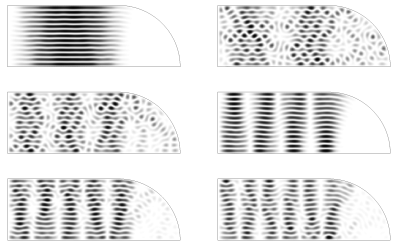
Stadium billiards
|
Another recent advance by Andrew Hassell is concerned with
this equidistribution question for eigenstates on a "stadium".
The classical mechanics of this system, that is the billiard ball motion in such a stadium, is not strongly chaotic (in the sense needed for the QUE conjecture) and in particular there is the family of periodic orbits which correspond to a billiard ball bouncing back and forth between the parallel sides of the stadium. From the beginning numerical calculations suggested that for this stadium there is a relatively sparse sequence of eigenstates that don't become equidistributed and which correspond to these bouncing balls. A proof of the existence of these bouncing ball modes is what Hassell has achieved. |

A typical wave function. Image from Douglas Stone's website
|
Arithmetic surfaces
The setting in which substantial progress has been made on these questions of the behaviour of highly excited states in a chaotic hamiltonian, is that corresponding to the geodesic motion a manifold of negative curvature which is furthermore arithmetic (the study of these problems in these cases is known as "arithmetic quantum chaos"). This of course is a very special type of manifold but it is one for which modern techniques from number theory and automorphic forms can be used effectively to investigate the eigenstates. The important feature defining these manifolds is an infinite family of pseudo-symmetries known as correspondences. These give rise to geometric operators that commute with the quantization of the Hamiltonian and in this setting one naturally assumes that the quantized states are also eigenstates of these geometric "Hecke Operators". For these there is by now a good understanding of the many of basic problems. In particular the formula of Thomas Watson, which explicitly connects periods of these eigenstates with the theory of L-functions, is central to much of the progress. For example the QUE conjecture follows for these states from something quite a bit weaker than the Riemann Hypothesis for the corresponding L-functions (precisely "subconvexity" suffices). Moreover the natural and interesting analogues of the QUE conjecture, that is the equidistribution of mass of the norms of such holomorphic hecke eigenforms (these are arithmetically perhaps the most interesting modular forms) would also follow from the corresponding subconvexity estimate.The QUE problem for such Hecke states is now all but completely settled for the case of arithmetic hyperbolic surfaces. First for compact such surfaces and for eigenstates of the quantized hamiltonian (that is the Laplacian), QUE was proven a few years ago by Elon Lindenstrauss. His proof introduces novel ideas from ergodic theory, specifically measure rigidity on homogeneous spaces (that is the classification of measures on such spaces which are invariant under certian diagonal subgroups), into the analysis of quantum limits. While this approach has been extended to handle the QUE conjecture for some higher dimensional arithmetic manifolds (by Silberman and Venkatesh) it has not succeeded in dealing with the analogue QUE problem for holomorphic forms nor for noncompact arithmetic surfaces.
Many of the missing cases have now been resolved by Holowinsky and Soundararajan. They have established the QUE conjecture for holomorphic forms of increasing weight (this is the semiclassical limit in this setting) for holomorphic Hecke forms on noncompact arithmetic surfaces. It is known in general for compact complex manifolds [Nonnenmacher-Voros, Shiffman-Zelditch] and in the pertinent noncompact surface case[Rudnick], that the equidistribution of mass of the norm of holomorphic sections of large powers of a positive line bundle implies the equidistribution of its zeros. Thus the zeros of a holomorphic Hecke eigenform on a noncompact arithmetic surface become equidistributed with respect to the hyperbolic area, as the weight goes to infinity. The last is a fundamental equidistribution property in the arithmetic theory of modular forms and is of independent interest.
The result of Holowinsky and Soundararajan comes from their separate attacks on the holomorphic QUE problem. Each method achieves the desired result up to a small number of exceptions. Remarkably their approaches are sufficiently different so that the set of exceptions to both approaches, is empty! Their proof relies heavily on the Ramanujan Conjectures which were established for such holomorphic forms by Deligne in the 70's.
What remains unresolved as far as QUE in the case of arithmetic surfaces, is the case of holomorphic forms on compact arithmetic surfaces and of eigenstates of the Laplacian in the noncompact such surfaces.
A mathematical model setting for studying quantizations and semiclassical limits is that of "quantizations "of symplectic maps. The special chaotic case of a linear area preserving map of the two torus (ie an element of SL(2,Z) whose trace has absolute value bigger than 2) goes by the name "a cat map". The states of the corresponding quantization can be studied in depth. It turns out that in this setting of cat maps, QUE can fail (Faure-Nonnenmacher-De Bievre). Some take this as a warning about the truth of the original QUE conjecture.
10/3/08