Graph catalog: Spectra of small graphs

Version: April 11, 2007

order 3 graphs

order 4 graphs

order 5 graphs

order 6 graphs

Petersen graph

4-antiprism

Barioli-Fallat counterexample to IEPG

pentasun

Main Index

Index of graphs
Description of graph entries
Graph operations
Parameter relationships
References
The catalog

This catalog provides information about the minimum rank and other graph parameters for specific small connected graphs. For families, please see the families catalog. For general background on the minimum rank problem, please see [FH]. Proofs of the results in the catalog can be found in the references cited in the catalog.

This catalog was developed through the American Institute of Mathematics workshop, "Spectra of Families of Matrices described by Graphs, Digraphs, and Sign Patterns," and is hosted by AIM. It is edited by Jason Grout, Leslie Hogben, Hein van der Holst and Amy Wangsness. The web-page was designed by David Farmer.

Please refer any questions or comments about the content of the catalog, including corrections or suggestions for additional information, to Leslie Hogben (lhogben(())iastate.edu) or one of the editors. Please refer any questions or comments about the operation of this web-site to David Farmer (farmer(())aimath.org).

The new information in this catalog is based on research done by the following people at the AIM workshop: Francesco Barioli, Wayne Barrett, Avi Berman, Richard Brualdi, Steven Butler, Sebastian Cioaba, Dragos Cvetkovic, Jane Day, Louis Deaett, Luz DeAlba, Shaun Fallat, Shmuel Friedland, Chris Godsil, Jason Grout, Willem Haemers, Leslie Hogben, In-Jae Kim, Steve Kirkland, Raphael Loewy, Judith McDonald, Rana Mikkelson, Sivaram Narayan, Olga Pryporova, Uri Rothblum, Irene Sciriha, Bryan Shader, Wasin So, Dragan Stevanovic, Pauline van den Driessche, Hein van der Holst, Kevin Vander Meulen, Amy Wangsness, Amy Yielding and on the work of Kaela Rasmussen.

Entries in the catalog

A typical entry in this catalog includes the following information for the graph or family of graphs.

Symbol name	Common names/symbols are used to describe a graph G in the family. Sometimes a graph operation is used.
picture	A picture of the graph, or a representative example from the family.
graph6	Code describing the adjacency matrix.
order	The number of vertices in the graph
mr	For a real symmetric matrix A, the graph of A, denoted G(A), is the graph with vertices {1,...,n } and edges { {i,j } \| a_ij ≠ 0 and i ≠ j } (note that the diagonal of A is ignored in determining G(A)). The minimum rank of G is mr(G)=min{rank(A) : A ∈ R^n×n, A^T=A, and G(A)=G}.
M	The maximum nullity (= maximum multiplicity of an eigenvalue) of a real symmetric matrix A such that G(A)=G
field independent	Minimum rank can be defined for symmetric matrices over any field. ``Yes" means the minimum rank of G is the same for all fields.
ξ	A real symmetric matrix M satisfies the Strong Arnold Hypothesis provided there does not exist a nonzero symmetric matrix X satisfying: MX = 0, M ° X = 0, I ° X=0, where ° denotes the Hadamard (entrywise) product and I is the identity matrix. The Colin de Veriere-type parameter ξ(G) is the maximum multiplicity of 0 as an eigenvalue among symmetric real matrices that satisfy G(A )=G and A satisfies the Strong Arnold Hypothesis.
ω	The largest value of m for which G has a clique of order m (subgraph isomorphic to K_m) is called the clique number of G and denoted by ω(G).
δ	The minimum degree of a vertex of G is denoted by δ(G).
tw	A tree-decomposition of a graph G=(V,E) is a pair (T,W), where T is a tree and W={W_t : t∈ V(T)} is a family of subsets of V with the properties: ∪ {W_t : t∈ V(T)}=V, for every edge e∈ E, there is a t∈V(T) such that has both ends of e are in W_t, and if t₁,t₂,t₃∈ V(T) and t₂ lies on the path from t₁ to t₃ in T, then W_t₁∩W_t₃⊆W_t₂. The width of a tree-decomposition is max{\|W_t\| - 1 : t∈ V(T)}. The tree-width of G, denoted by tw(G), is the minimum possible width of a tree-decomposition of G.
cc	Clique covering number, or Cliquecover. A set of subgraphs of G, each of which is a clique and such that every edge of G is contained in at least one of these cliques, is called a clique covering of G. The clique covering number of G, denoted by cc(G), is the smallest number of cliques in a clique covering of G.
diam	The distance between two vertices in a graph G is the number of edges in a shortest path between them. The diameter of G, diam(G), is the maximum distance between any two vertices of G.
maxinducedpath	The maximum number of edges in a path that is an induced subgraph of G.
Z	Color-change rule: If G is a graph with each vertex colored either white or black, u is a black vertex of G, and exactly one neighbor v of u is white, then change the color of v to black. Given a coloring of G, the derived coloring is the result of applying the color-change rule until no more changes result. A zero forcing set for a graph G is a subset of vertices Z such that if initially the vertices in Z are colored black and the remaining vertices are colored white, the derived coloring of G is all black. Z(G) is the minimum of \|Z\| over all zero forcing sets Z⊆ V(G).
α	An induced subgraph H of a graph G is a coclique or independent set of vertices if H has no edges. The largest value of m for which a coclique with m vertices exists is called the vertex independence number of G and denoted by α(G).

Notes:	Any other comments.

Graph operations

The following graph operations are used to construct families:

The complement of a graph G=(V,E) is the graph G = (V,E), where E consists of all two element sets from V that are not in E.
The line graph of a graph G=(V,E), denoted L(G), is the graph having vertex set E, with two vertices in L(G) adjacent if and only if the corresponding edges are adjacent in G.
The Cartesian product of two graphs G and H, denoted G ☐ H, is the graph with vertex set V(G) × V(H) such that (u,v) is adjacent to (u',v') if and only if
(1) u=u' and vv' ∈ E(H),
or
(2) v=v' and uu' ∈ E(G).
The strong product of two graphs G and H, denoted G ⊠ H, is the graph with vertex set V(G) × V(H) such that (u,v) is adjacent to (u',v') if and only if
(1) uu' ∈ E(G) and vv' ∈ E(H),
or
(2) u=u' and vv' ∈ E(H),
or
(3) v=v' and uu' ∈ E(G).
The corona of G with H, denoted G ° H, is the graph of order |G||H| + |G| obtained by taking one copy of G and |G| copies of H, and joining all the vertices in the ith copy of H to the ith vertex of G.

Parameter Relationships

The following relationships between the parameters are known:

mr(G) + M(G) = |G| (where |G| denotes the order of G)
M(G) ≤ Z(G) [AIM]
ξ(G) ≤ M(G) [BFH3]
ω(G) -1 ≤ ξ(G) [BFH3]
δ(G) ≤ tw(G)
mr(G) ≤ cc(G)
diam(G) ≤ maxinducedpath(G) ≤ mr(G)
ξ(G) ≤ |G| - α(G) + 1 [BFH3]

References

[AIM] AIM Minimum rank - special graphs work group. Zero forcing sets and the minimum rank of graphs. Preprint.

[BFH] F. Barioli, S. Fallat, and L. Hogben. Computation of minimal rank and path cover number for graphs. Linear Algebra and Its Applications, 392: 289--303, 2004.

[BFH2] F. Barioli, S. Fallat, and L. Hogben. On the difference between the maximum multiplicity and path cover number for tree-like graphs. Linear Algebra and Its Applications 409: 13--31, 2005.

[BFH3] F. Barioli, S. Fallat, and L. Hogben. A variant on the graph parameters of Colin de Verdi`ere: Implications to the minimum rank of graphs. Electronic Journal of Linear Algebra, 13: 387--404, 2005.

[BHL2] W. Barrett, H. van der Holst and R. Loewy. Graphs whose minimal rank is two: The finite fields case. Electronic Journal of Linear Algebra, 14: 32--42, 2005.

[BvdHL] W. Barrett, H. van der Holst and R. Loewy. Graphs whose minimal rank is two. Electronic Journal of Linear Algebra, 11: 258--280, 2004.

[FH] S. Fallat and L. Hogben. The Minimum Rank of Symmetric Matrices Described by a Graph: A Survey. Preprint.

[H] L. Hogben. Spectral graph theory and the inverse eigenvalue problem of a graph. Electronic Journal of Linear Algebra, 14:12-31, 2005.

[H2] L. Hogben. Orthogonal representations, minimum rank, and graph complements. Preprint. Available at http://orion.math.iastate.edu/lhogben/research/Hogbenminrank07.pdf

[HvdH] L. Hogben and H. van der Holst. Forbidden minors for the class of graphs G with ξ(G) ≤ 2. To appear in Linear Algebra and Its Applications.

[JLD] C. R. Johnson and A. Leal Duarte. The maximum multiplicity of an eigenvalue in a matrix whose graph is a tree. Linear and Multilinear Algebra 46: 139--144, 1999.

[JS] C. R. Johnson and C. M. Saiago. Estimation of the maximum multiplicity of an eigenvalue in terms of the vertex degrees of the graph of the matrix. Electronic Journal of Linear Algebra, 9:27--31, 2002.

Catalog of graphs

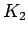, Complete graph on 2 vertices
graph6 :	A_
Order :	2
mr :	1
M :	1
field independent :	yes
ξ :	1
ω :	2
δ :	1
tw :	1
cc :	1
Diameter :	1
maxinducedpath :	1
Z :	1
α :	1
G name :	G3

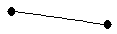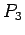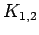, $K_{1,2}$ Path on 3 vertices
graph6 :	Bg
Order :	3
mr :	2
M :	1
field independent :	yes
ξ :	1
ω :	2
δ :	1
tw :	1
cc :	2
Diameter :	2
maxinducedpath :	2
Z :	1
α :	2
G name :	G6

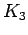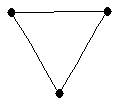
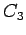, Complete graph on 3 vertices
graph6 :	Bw
Order :	3
mr :	1
M :	2
field independent :	yes
ω :	3
δ :	2
tw :	2
cc :	1
Diameter :	1
maxinducedpath :	1
Z :	2
α :	1
G name :	G7

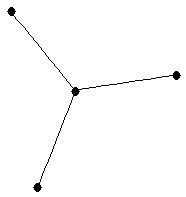
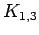$K_{1,3}$ Star on 4 vertices
graph6 :	Cs
Order :	4
mr :	2
M :	2
field independent :	yes
ξ :	2
ω :	2
δ :	1
tw :	1
cc :	3
Diameter :	2
maxinducedpath :	2
Z :	2
α :	3
G name :	G13
Notes :	tree

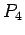Path on 4 vertices
graph6 :	Ch
Order :	4
mr :	3
M :	1
field independent :	yes
ξ :	1
ω :	2
δ :	1
tw :	1
cc :	3
Diameter :	3
maxinducedpath :	3
Z :	1
α :	2
G name :	G14

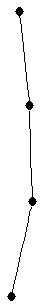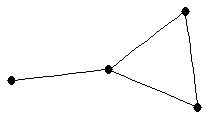
paw
graph6 :	Cj
Order :	4
mr :	2
M :	2
field independent :	yes
ξ :	2
ω :	3
δ :	1
cc :	2
Diameter :	2
maxinducedpath :	2
Z :	2
α :	2
G name :	G15

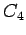4-cycle
graph6 :	Cl
Order :	4
mr :	2
M :	2
field independent :	yes
ξ :	2
ω :	2
δ :	2
tw :	2
cc :	4
Diameter :	2
maxinducedpath :	2
Z :	2
α :	2
G name :	G16
Notes :	References: [BvdHL], [BvdHL2]

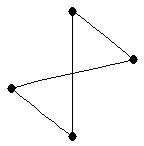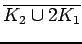$\overline{K_2\cup 2K_1}$ diamond or kite
graph6 :	Cz
Order :	4
mr :	2
M :	2
field independent :	yes
ξ :	2
ω :	3
δ :	2
tw :	2
cc :	2
Diameter :	2
maxinducedpath :	2
Z :	2
α :	2
G name :	G17
Notes :	linear 2-tree

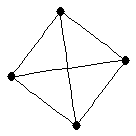
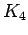Complete graph on 4 vertices
graph6 :	C~
Order :	4
mr :	1
M :	3
field independent :	yes
ξ :	3
ω :	4
δ :	3
tw :	3
cc :	1
Diameter :	1
maxinducedpath :	1
Z :	3
α :	1
G name :	G18

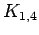$K_{1,4}$ Star on 5 vertices
graph6 :	Ds_
Order :	5
mr :	2
M :	3
field independent :	yes
ξ :	2
ω :	2
δ :	1
tw :	1
cc :	4
Diameter :	2
maxinducedpath :	2
Z :	3
α :	4
G name :	G29
Notes :	tree

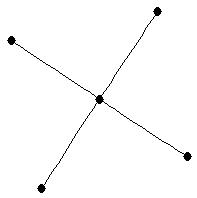Chair or Generalized star on 5 vertices
graph6 :	DsC
Order :	5
mr :	3
M :	2
field independent :	yes
ξ :	2
ω :	2
δ :	1
tw :	1
cc :	4
Diameter :	3
maxinducedpath :	3
Z :	2
α :	3
G name :	G30
Notes :	tree References: [FH] (field independence) [BFH3] (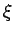 $\xi$ )

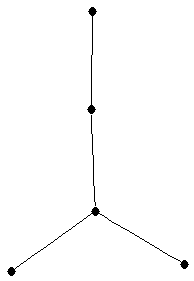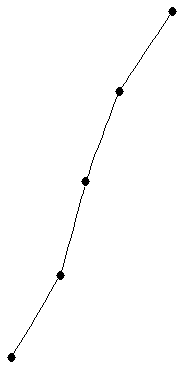
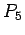Path on 5 vertices
graph6 :	DhC
Order :	5
mr :	4
M :	1
field independent :	yes
ξ :	1
ω :	2
δ :	1
tw :	1
cc :	4
Diameter :	4
maxinducedpath :	4
Z :	1
α :	3
G name :	G31

Fish
graph6 :	DXK
Order :	5
mr :	3
M :	2
field independent :	yes
ξ :	2
ω :	3
δ :	1
tw :	2
cc :	3
Diameter :	2
maxinducedpath :	2
α :	3
G name :	G34
Notes :	forbidden for mr=2 References: [FH] (field independence - cut-vertex) [BFH3] (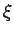 $\xi$ )

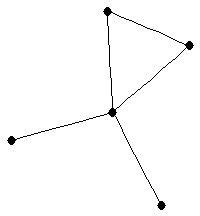bull
graph6 :	Dgs
Order :	5
mr :	3
M :	2
field independent :	yes
ξ :	2
ω :	3
δ :	1
cc :	3
Diameter :	3
maxinducedpath :	3
Z :	2
α :	3
G name :	G35
Notes :	References: [FH] (field independence - cut-vertex) [BFH3] (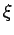 $\xi$ )


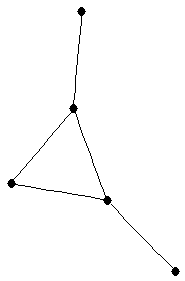graph6 :	DhK
Order :	5
mr :	3
M :	2
field independent :	yes
ξ :	2
ω :	3
δ :	1
cc :	3
Diameter :	3
maxinducedpath :	3
Z :	2
α :	3
G name :	G36
Notes :	References: [FH] (field independence - cut-vertex) [BFH3] (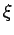 $\xi$ )


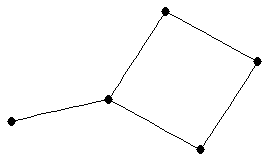
graph6 :	DhS
Order :	5
mr :	3
M :	2
field independent :	yes
ξ :	2
ω :	2
δ :	1
cc :	5
Diameter :	3
maxinducedpath :	3
Z :	2
α :	3
G name :	G37
Notes :	References: [FH] (field independence - cut-vertex) [BFH3] (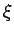 $\xi$ )

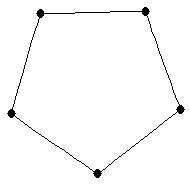
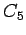5-cycle
graph6 :	Dhc
Order :	5
mr :	3
M :	2
field independent :	yes
ξ :	2
ω :	2
δ :	2
tw :	2
cc :	5
Diameter :	2
maxinducedpath :	3
α :	2
G name :	G38

Dart
graph6 :	DjS
Order :	5
mr :	3
M :	2
field independent :	yes
ξ :	2
ω :	3
δ :	1
tw :	2
cc :	3
Diameter :	2
maxinducedpath :	2
Z :	2
α :	3
G name :	G40
Notes :	forbidden for mr=2 References: [FH] (field independence - cut-vertex) [BFH3] (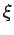 $\xi$ )


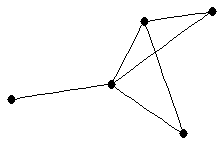
graph6 :	Dh[
Order :	5
mr :	3
M :	2
field independent :	yes
ξ :	2
ω :	3
δ :	1
cc :	3
Diameter :	3
maxinducedpath :	3
Z :	2
α :	2
G name :	G41
Notes :	References: [FH] (field independence - cut-vertex) [BFH3] (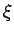 $\xi$ )

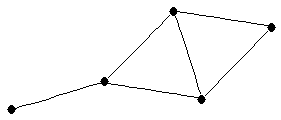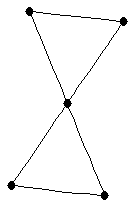
bowtie
graph6 :	DxK
Order :	5
mr :	2
M :	3
field independent :	yes
ξ :	2
ω :	3
δ :	2
tw :	2
cc :	2
Diameter :	2
maxinducedpath :	2
Z :	3
α :	2
G name :	G42
Notes :	References: [BFH3] (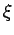 $\xi$ )

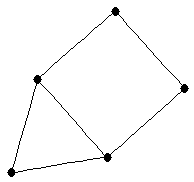
house
graph6 :	Dhs
Order :	5
mr :	3
M :	2
field independent :	yes
ξ :	2
ω :	3
δ :	2
tw :	2
cc :	4
Diameter :	2
maxinducedpath :	3
Z :	2
α :	2
G name :	G43
Notes :	"linear 2-tree" (not a 2-tree) References: [HvdH]

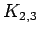$K_{2,3}$ complete bipartite graph on 2,3 vertices
graph6 :	DlS
Order :	5
mr :	2
M :	3
field independent :	yes
ξ :	3
ω :	2
δ :	2
cc :	6
Diameter :	2
maxinducedpath :	2
Z :	3
α :	2
G name :	G44
Notes :	References: [BFH3] (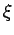 $\xi$ )


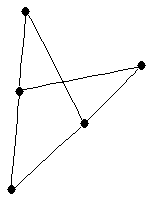graph6 :	Dj[
Order :	5
mr :	2
M :	3
field independent :	yes
ξ :	3
δ :	1
cc :	2
Diameter :	2
maxinducedpath :	2
Z :	3
α :	2
G name :	G45
Notes :	References: [FH] (field independence - cut-vertex) [BFH3] (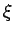 $\xi$ )


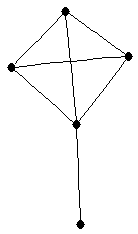graph6 :	DnS
Order :	5
mr :	2
M :	3
field independent :	yes
ξ :	3
ω :	3
δ :	2
cc :	3
Diameter :	2
maxinducedpath :	2
Z :	3
α :	3
G name :	G46
Notes :	2-tree References: [HvdH] (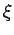 $\xi$ )


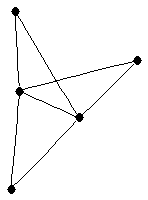graph6 :	Dls
Order :	5
mr :	2
M :	3
field independent :	yes
ξ :	3
ω :	3
δ :	2
cc :	4
Diameter :	2
maxinducedpath :	2
Z :	3
α :	2
G name :	G48
Notes :	References: [BvdHL], [BvdHL2]

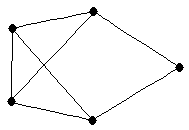full house
graph6 :	Dns
Order :	5
mr :	2
M :	3
field independent :	no (see notes)
ξ :	3
ω :	4
δ :	2
tw :	3
cc :	2
Diameter :	2
maxinducedpath :	2
Z :	3
α :	2
G name :	G49
Notes :	minimum rank over 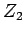is 3. References: [BvdHL], [BvdHL2]

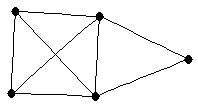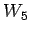Wheel
graph6 :	Dl{
Order :	5
mr :	2
M :	3
field independent :	yes
ξ :	3
ω :	3
δ :	3
cc :	4
Diameter :	2
maxinducedpath :	2
Z :	3
α :	2
G name :	G50
Notes :	Reference: [BvdHL], [BvdHL2]

$\overline{K_2 \cup 3K_1}$
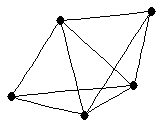
graph6 :	Dn{
Order :	5
mr :	2
M :	3
field independent :	yes
ξ :	3
ω :	4
δ :	3
tw :	3
cc :	2
Diameter :	2
maxinducedpath :	2
Z :	3
α :	2
G name :	G51
Notes :	References: [BvdHL], [BvdHL2]

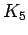Complete graph on 5 vertices
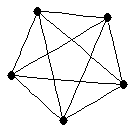
graph6 :	D~{
Order :	5
mr :	1
M :	4
field independent :	yes
ξ :	4
ω :	5
δ :	4
tw :	4
cc :	1
Diameter :	1
maxinducedpath :	1
Z :	4
α :	1
G name :	G52

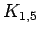$K_{1,5}$ star on 6 vertices
graph6 :	Esa?
Order :	6
mr :	2
M :	4
field independent :	yes
ξ :	2
ω :	2
δ :	1
tw :	1
cc :	5
Diameter :	2
maxinducedpath :	2
Z :	4
α :	5
G name :	G77
Notes :	tree


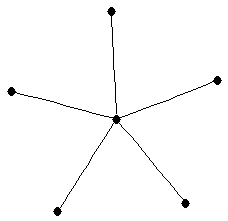graph6 :	E?Fg
Order :	6
mr :	3
M :	3
field independent :	yes
ξ :	2
ω :	2
δ :	1
tw :	1
cc :	5
Diameter :	3
maxinducedpath :	3
Z :	3
α :	4
G name :	G78
Notes :	tree References: [FH] (field independence) [BFH3] (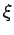 $\xi$ )


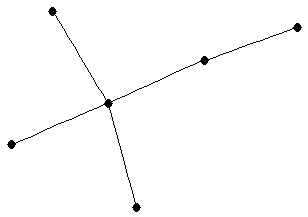graph6 :	E?dg
Order :	6
mr :	4
M :	2
field independent :	yes
ξ :	2
ω :	2
δ :	1
cc :	5
Diameter :	3
maxinducedpath :	3
Z :	3
α :	4
G name :	G79
Notes :	tree References: [FH] (field independence) [BFH3] (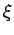 $\xi$ )


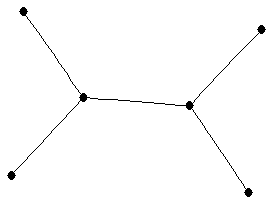graph6 :	EhGG
Order :	6
mr :	4
M :	2
field independent :	yes
ξ :	2
ω :	2
δ :	1
tw :	1
cc :	5
Diameter :	4
maxinducedpath :	4
Z :	2
α :	3
G name :	G80
Notes :	tree References: [FH] (field independence) [BFH3] (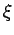 $\xi$ )


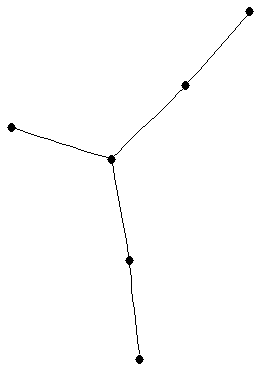graph6 :	EXCG
Order :	6
mr :	4
M :	2
field independent :	yes
ξ :	2
ω :	2
δ :	1
tw :	1
cc :	5
Diameter :	4
maxinducedpath :	4
Z :	2
α :	4
G name :	G81
Notes :	tree References: [FH] (field independence) [BFH3] (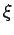 $\xi$ )

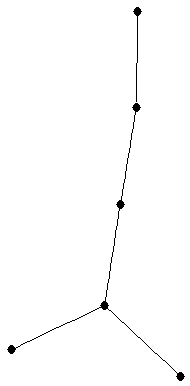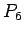path on 6 vertices
graph6 :	EhCG
Order :	6
mr :	5
M :	1
field independent :	yes
ξ :	1
ω :	2
δ :	1
tw :	1
cc :	5
Diameter :	5
maxinducedpath :	5
Z :	1
α :	3
G name :	G83


graph6 :	EFCW
Order :	6
mr :	3
M :	3
ω :	3
δ :	1
cc :	4
Diameter :	2
Z :	3
G name :	G92


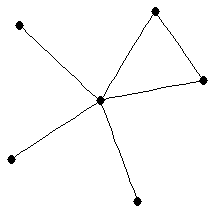graph6 :	EiSG
Order :	6
mr :	4
M :	2
ω :	3
δ :	1
cc :	4
Diameter :	3
Z :	2
G name :	G93

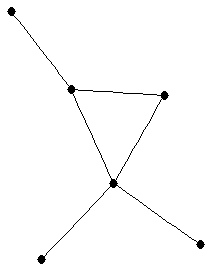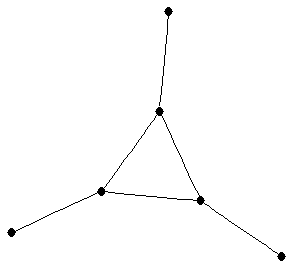
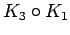$K_3\circ K_1$ corona of 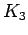with 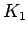(3-sun)
graph6 :	Ex`?
Order :	6
mr :	4
M :	2
field independent :	yes
ξ :	2
ω :	3
δ :	1
tw :	2
cc :	4
Diameter :	3
maxinducedpath :	3
Z :	4
α :	3
G name :	G94
Notes :	References: [BFH], [FH]


graph6 :	EhPG
Order :	6
mr :	4
M :	2
ω :	3
δ :	1
cc :	4
Diameter :	3
Z :	2
G name :	G95


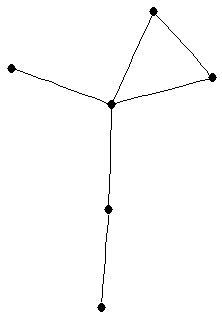graph6 :	EXCg
Order :	6
mr :	4
M :	2
ω :	2
δ :	1
cc :	6
Diameter :	3
Z :	2
G name :	G96


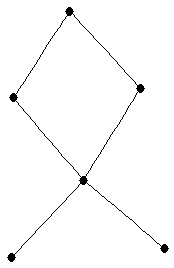graph6 :	EjCG
Order :	6
mr :	4
M :	2
ω :	3
δ :	1
cc :	4
Diameter :	4
Z :	2
G name :	G97


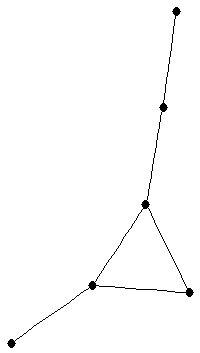graph6 :	EhSG
Order :	6
mr :	4
M :	2
ω :	2
δ :	1
cc :	6
Diameter :	3
Z :	2
G name :	G98


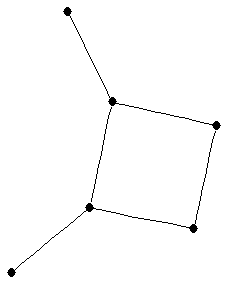graph6 :	EhDO
Order :	6
mr :	4
M :	2
ω :	2
δ :	1
cc :	6
Diameter :	4
Z :	2
G name :	G99


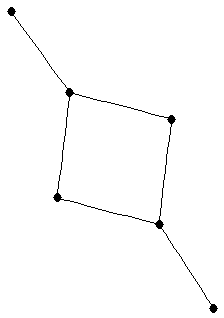graph6 :	ExCO
Order :	6
mr :	3
M :	3
ω :	3
δ :	1
cc :	4
Diameter :	3
Z :	3
G name :	G100


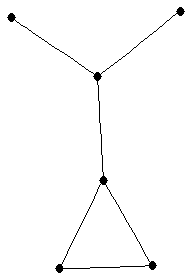graph6 :	ExCG
Order :	6
mr :	4
M :	2
ω :	3
δ :	1
cc :	4
Diameter :	4
Z :	2
G name :	G102


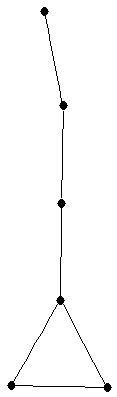graph6 :	ElCG
Order :	6
mr :	4
M :	2
ω :	2
δ :	1
cc :	6
Diameter :	4
Z :	2
G name :	G103


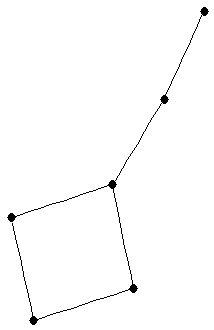graph6 :	EhDG
Order :	6
mr :	4
M :	2
ω :	2
δ :	1
cc :	6
Diameter :	3
Z :	2
G name :	G104

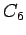6-cycle
graph6 :	EhEG
Order :	6
mr :	4
M :	2
field independent :	yes
ξ :	2
ω :	2
δ :	2
tw :	2
cc :	6
Diameter :	3
maxinducedpath :	4
Z :	2
α :	3
G name :	G105


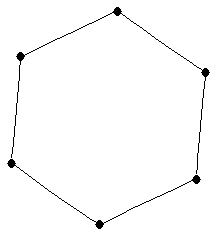
graph6 :	EiPW
Order :	6
mr :	4
M :	2
ω :	3
δ :	1
cc :	4
Diameter :	2
Z :	2
G name :	G111


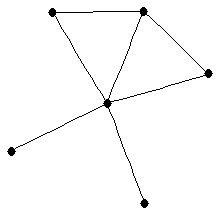graph6 :	EjSO
Order :	6
mr :	4
M :	2
ω :	3
δ :	1
cc :	4
Diameter :	3
Z :	2
G name :	G112


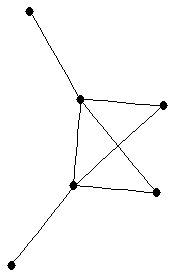
graph6 :	Eh[G
Order :	6
mr :	4
M :	2
field independent :	yes
ω :	3
δ :	1
cc :	4
Diameter :	3
maxinducedpath :	3
Z :	2
G name :	G113


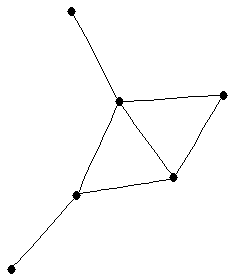graph6 :	EiSW
Order :	6
mr :	3
M :	3
ω :	3
δ :	1
cc :	4
Diameter :	3
Z :	3
G name :	G114


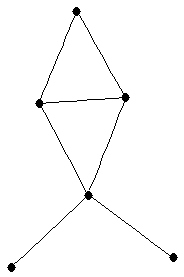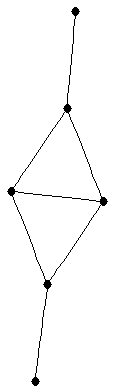
graph6 :	EjKG
Order :	6
mr :	4
M :	2
ω :	3
δ :	1
cc :	4
Diameter :	4
Z :	2
G name :	G115


graph6 :	ExK_
Order :	6
mr :	3
M :	3
ω :	3
δ :	1
cc :	3
Diameter :	2
Z :	3
G name :	G117


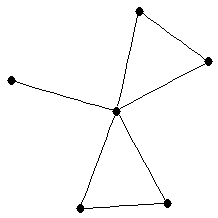graph6 :	EhTG
Order :	6
mr :	4
M :	2
ω :	3
δ :	1
cc :	5
Diameter :	3
Z :	2
G name :	G118


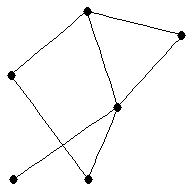graph6 :	ExKG
Order :	6
mr :	3
M :	3
ω :	3
δ :	1
cc :	3
Diameter :	3
Z :	3
G name :	G119


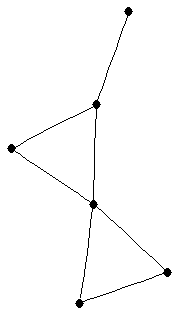graph6 :	EhGw
Order :	6
mr :	4
M :	2
ω :	3
δ :	1
cc :	4
Diameter :	3
Z :	2
G name :	G120


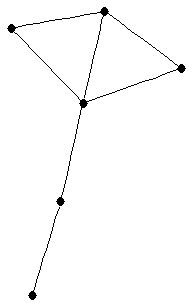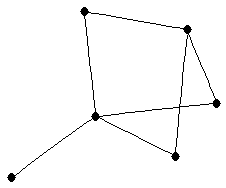
graph6 :	EhTO
Order :	6
mr :	3
M :	3
ω :	2
δ :	1
cc :	7
Diameter :	3
Z :	3
G name :	G121


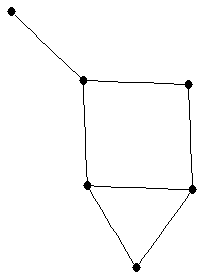
graph6 :	EyKG
Order :	6
mr :	4
M :	2
ω :	3
δ :	1
cc :	5
Diameter :	3
Z :	2
G name :	G122


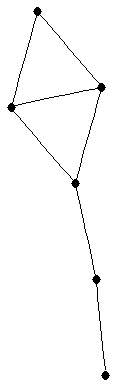
graph6 :	EhKW
Order :	6
mr :	4
M :	2
ω :	3
δ :	1
cc :	4
Diameter :	4
Z :	2
G name :	G123


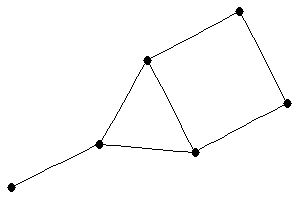
graph6 :	EhDg
Order :	6
mr :	4
M :	2
ω :	3
δ :	1
cc :	5
Diameter :	3
Z :	2
G name :	G124


graph6 :	EhHW
Order :	6
mr :	3
M :	3
ω :	2
δ :	1
cc :	7
Diameter :	3
Z :	3
G name :	G125


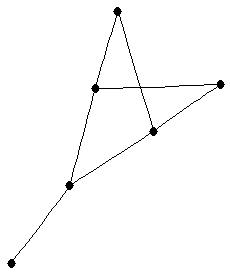graph6 :	ElCW
Order :	6
mr :	3
M :	3
field independent :	yes
ξ :	2
ω :	3
δ :	2
cc :	5
Diameter :	3
maxinducedpath :	3
Z :	3
α :	3
G name :	G126
Notes :	References: [FH] (field independence - cut-vertex) [HvdH] (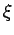 $\xi$ )


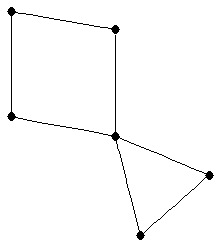graph6 :	ExEG
Order :	6
mr :	4
M :	2
field independent :	yes
ξ :	2
ω :	3
δ :	2
tw :	2
cc :	5
Diameter :	3
maxinducedpath :	4
Z :	2
α :	3
G name :	G127
Notes :	"linear 2-tree" (not a 2-tree) References: [HvdH]


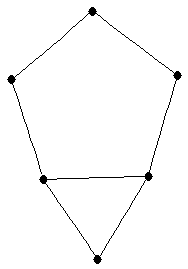graph6 :	ElEG
Order :	6
mr :	4
M :	2
ξ :	2
ω :	2
δ :	2
cc :	7
Diameter :	3
maxinducedpath :	4
Z :	2
α :	3
G name :	G128
Notes :	"linear 2-tree" (not a 2-tree) References: [HvdH]


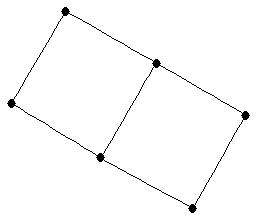graph6 :	Ehe_
Order :	6
mr :	3
M :	3
ω :	2
δ :	2
cc :	7
Diameter :	2
Z :	3
G name :	G129


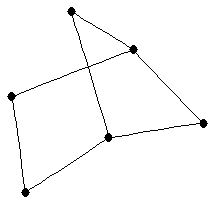graph6 :	ExCW
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	3
Diameter :	3
Z :	3
G name :	G130


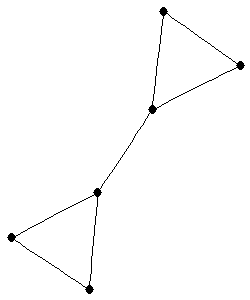graph6 :	EiTW
Order :	6
mr :	3
M :	3
ω :	4
δ :	1
cc :	3
Diameter :	2
Z :	3
G name :	G133


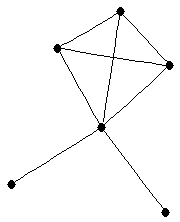graph6 :	EgvG
Order :	6
mr :	3
M :	3
ω :	4
δ :	1
cc :	3
Diameter :	3
Z :	3
G name :	G134


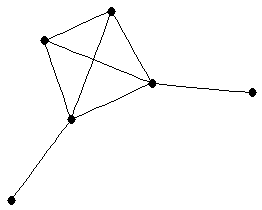graph6 :	Exi_
Order :	6
mr :	3
M :	3
ω :	3
δ :	1
cc :	4
Diameter :	2
Z :	3
G name :	G135


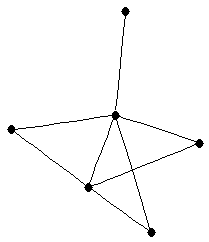graph6 :	Eh{G
Order :	6
mr :	4
M :	2
ω :	3
δ :	1
cc :	4
Diameter :	2
Z :	2
G name :	G136


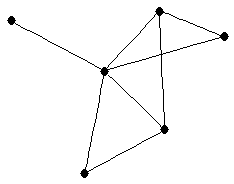graph6 :	EjFO
Order :	6
mr :	4
M :	2
ω :	3
δ :	1
cc :	4
Diameter :	3
Z :	2
G name :	G137


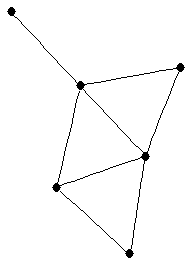graph6 :	Eh[g
Order :	6
mr :	3
M :	3
ω :	3
δ :	1
cc :	4
Diameter :	3
Z :	3
G name :	G138


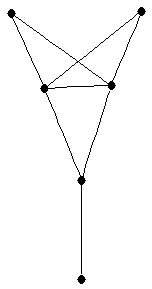graph6 :	Eh{O
Order :	6
mr :	4
M :	2
ω :	3
δ :	1
cc :	4
Diameter :	3
Z :	2
G name :	G139


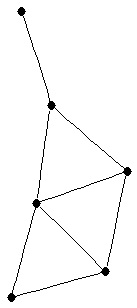graph6 :	EjSg
Order :	6
mr :	3
M :	3
ω :	3
δ :	1
cc :	5
Diameter :	3
Z :	3
G name :	G140


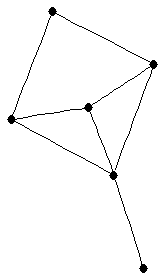graph6 :	EiLW
Order :	6
mr :	3
M :	3
field independent :	yes
ω :	3
δ :	1
cc :	5
Diameter :	3
maxinducedpath :	3
Z :	3
α :	3
G name :	G141


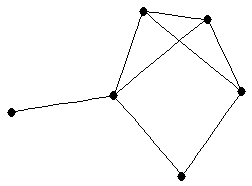graph6 :	EhKw
Order :	6
mr :	3
M :	3
ω :	4
δ :	1
cc :	3
Diameter :	3
Z :	3
G name :	G142


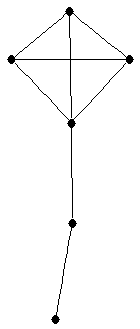graph6 :	EhSw
Order :	6
mr :	3
M :	3
ω :	3
δ :	1
cc :	5
Diameter :	3
Z :	3
G name :	G143


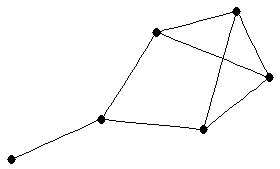graph6 :	ExKg
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	3
Diameter :	2
Z :	3
G name :	G144


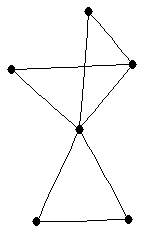graph6 :	Exe_
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	5
Diameter :	2
Z :	3
G name :	G145

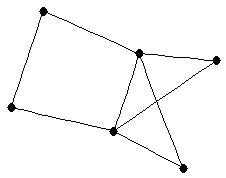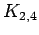$K_{2,4}$ complete bipartite graph on 2,4 vertices
graph6 :	Eli_
Order :	6
mr :	2
M :	4
field independent :	yes
ξ :	3
ω :	2
δ :	2
cc :	8
Diameter :	2
maxinducedpath :	2
Z :	4
α :	4
G name :	G146
Notes :	References: [BFH3] (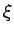 $\xi$ )


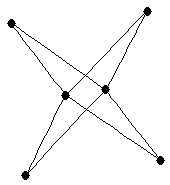graph6 :	EhVG
Order :	6
mr :	4
M :	2
field independent :	yes
ξ :	2
ω :	3
δ :	2
cc :	5
Diameter :	3
maxinducedpath :	4
Z :	2
α :	3
G name :	G147
Notes :	"linear 2-tree" (not a 2-tree) References: [HvdH]


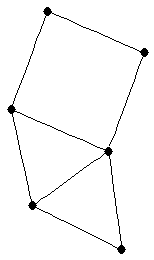graph6 :	ExeG
Order :	6
mr :	4
M :	2
field independent :	yes
ξ :	2
ω :	3
δ :	2
cc :	4
Diameter :	2
maxinducedpath :	4
Z :	2
α :	3
G name :	G148
Notes :	"linear 2-tree" (not a 2-tree) References: [HvdH]


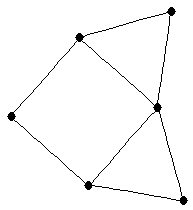graph6 :	EldO
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	6
Diameter :	2
Z :	3
G name :	G149


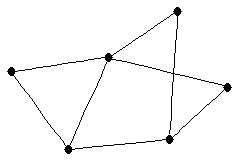graph6 :	ExKW
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	3
Diameter :	3
Z :	3
G name :	G150


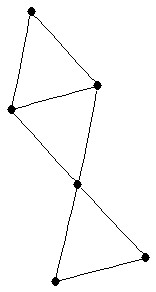graph6 :	Eheg
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	6
Diameter :	2
Z :	3
G name :	G151


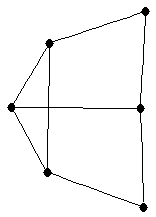graph6 :	EhNG
Order :	6
mr :	4
M :	2
field independent :	yes
ξ :	2
ω :	3
δ :	2
cc :	4
Diameter :	3
maxinducedpath :	3
Z :	2
α :	2
G name :	G152
Notes :	"linear 2-tree" (not a 2-tree) References: [HvdH]


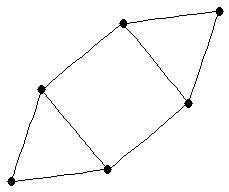graph6 :	Ehf_
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	5
Diameter :	2
Z :	3
G name :	G153


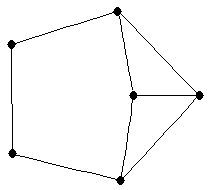graph6 :	EhUg
Order :	6
mr :	3
M :	3
ω :	2
δ :	2
cc :	8
Diameter :	3
Z :	3
G name :	G154


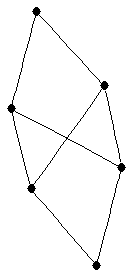graph6 :	Exy_
Order :	6
mr :	3
M :	3
ω :	4
δ :	1
cc :	3
Diameter :	2
Z :	3
G name :	G156


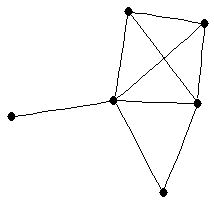graph6 :	Ej[g
Order :	6
mr :	3
M :	3
ω :	4
δ :	1
cc :	3
Diameter :	3
Z :	3
G name :	G157


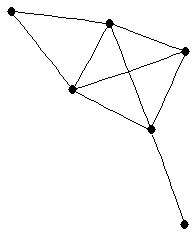graph6 :	Er{G
Order :	6
mr :	3
M :	3
ω :	3
δ :	1
cc :	5
Diameter :	2
Z :	3
G name :	G158


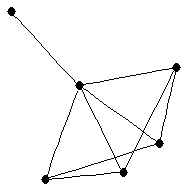graph6 :	Ei[w
Order :	6
mr :	3
M :	3
ω :	3
δ :	1
cc :	5
Diameter :	3
Z :	3
G name :	G159


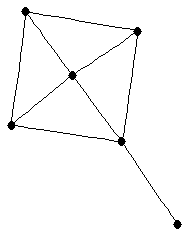graph6 :	ExFo
Order :	6
mr :	3
M :	3
ω :	4
δ :	1
cc :	3
Diameter :	3
Z :	3
G name :	G160


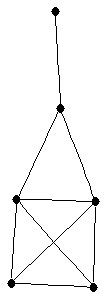graph6 :	EnTO
Order :	6
mr :	2
M :	4
ω :	3
δ :	2
cc :	4
Diameter :	2
Z :	4
G name :	G161


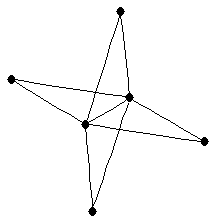graph6 :	EndO
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	4
Diameter :	2
Z :	3
G name :	G162

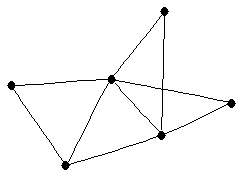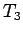3rd supertriangle
graph6 :	EjFW
Order :	6
mr :	3
M :	3
ξ :	3
ω :	3
δ :	2
cc :	3
Diameter :	2
maxinducedpath :	3
Z :	3
α :	3
G name :	G163
Notes :	References: [HvdH]


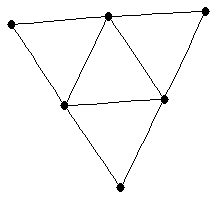graph6 :	ExMg
Order :	6
mr :	4
M :	2
field independent :	yes
ξ :	2
ω :	3
δ :	2
tw :	2
cc :	4
Diameter :	2
maxinducedpath :	4
Z :	2
α :	3
G name :	G164
Notes :	linear 2-tree References: [HvdH]


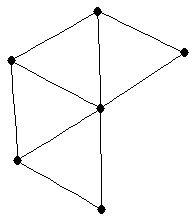graph6 :	ExKw
Order :	6
mr :	2
M :	4
ω :	4
δ :	2
cc :	2
Diameter :	2
Z :	4
G name :	G165


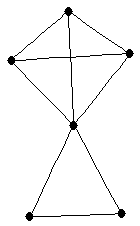graph6 :	EjdW
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	5
Diameter :	2
Z :	3
G name :	G166


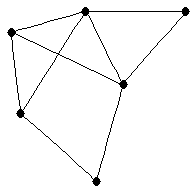graph6 :	EjuG
Order :	6
mr :	4
M :	2
field independent :	yes
ξ :	2
ω :	3
δ :	2
cc :	4
Diameter :	3
maxinducedpath :	3
Z :	2
α :	2
G name :	G167
Notes :	linear 2-tree References: [HvdH]


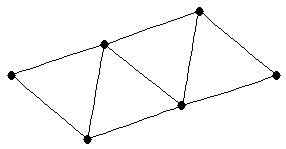graph6 :	EnUG
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	5
Diameter :	3
Z :	3
G name :	G168


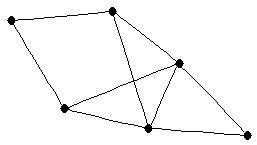graph6 :	Ej]G
Order :	6
mr :	3
M :	3
ω :	4
δ :	2
cc :	4
Diameter :	2
Z :	3
G name :	G169


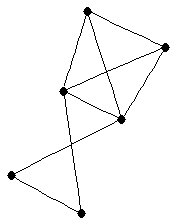graph6 :	Elig
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	6
Diameter :	2
Z :	3
G name :	G170


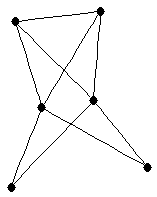graph6 :	Ehew
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	5
Diameter :	2
Z :	3
G name :	G171


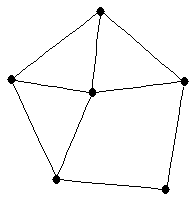graph6 :	Eldo
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	4
Diameter :	2
Z :	3
G name :	G172


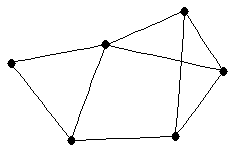
graph6 :	ElFg
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	6
Diameter :	2
Z :	3
G name :	G173

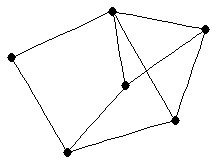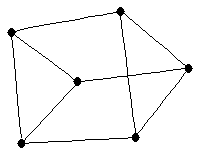
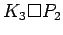$K_3\Box P_2$ 3-prism
graph6 :	Eldg
Order :	6
mr :	3
M :	3
field independent :	no (see notes)
ξ :	3
ω :	3
δ :	3
cc :	5
Diameter :	2
maxinducedpath :	3
Z :	3
α :	2
G name :	G174
Notes :	minimum rank is different for 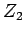Reference: [AIM]


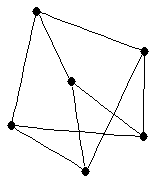
graph6 :	ElUg
Order :	6
mr :	2
M :	4
ω :	2
δ :	3
cc :	9
Diameter :	2
Z :	4
G name :	G175


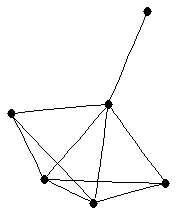
graph6 :	E\|{G
Order :	6
mr :	3
M :	3
ω :	4
δ :	1
cc :	3
Diameter :	2
Z :	3
G name :	G177


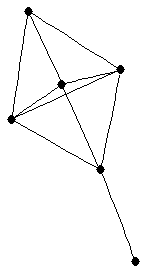
graph6 :	Ej[w
Order :	6
mr :	3
M :	3
ω :	4
δ :	1
cc :	3
Diameter :	3
Z :	3
G name :	G178


graph6 :	E~eO
Order :	6
mr :	3
M :	3
ω :	4
δ :	2
cc :	3
Diameter :	2
Z :	3
G name :	G179


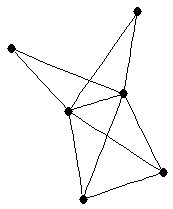graph6 :	EjVW
Order :	6
mr :	3
M :	3
ω :	4
δ :	2
cc :	3
Diameter :	2
Z :	3
G name :	G180


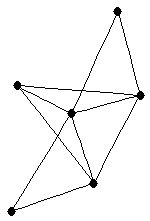graph6 :	EhZw
Order :	6
mr :	3
M :	3
ω :	4
δ :	2
cc :	3
Diameter :	3
Z :	3
G name :	G181


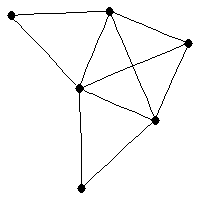graph6 :	El\|G
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	5
Diameter :	2
Z :	3
G name :	G182


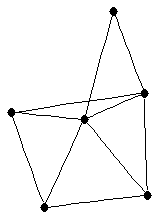graph6 :	Eh~G
Order :	6
mr :	3
M :	3
ω :	4
δ :	2
cc :	3
Diameter :	2
Z :	3
G name :	G183


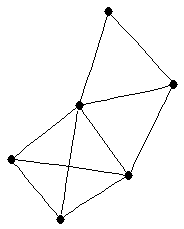graph6 :	EjfW
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	4
Diameter :	2
Z :	3
G name :	G184


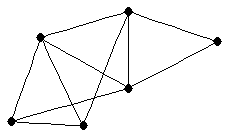graph6 :	E\|lG
Order :	6
mr :	3
M :	3
ω :	4
δ :	2
cc :	4
Diameter :	2
Z :	3
G name :	G185


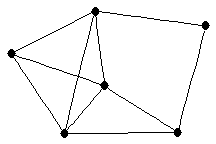graph6 :	Elmg
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	6
Diameter :	2
Z :	3
G name :	G186


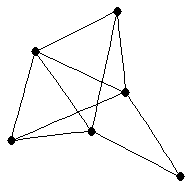graph6 :	Ehfw
Order :	6
mr :	3
M :	3
ω :	3
δ :	3
cc :	5
Diameter :	2
Z :	3
G name :	G187


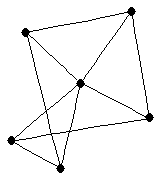
graph6 :	El^_
Order :	6
mr :	3
M :	3
ω :	3
δ :	3
cc :	5
Diameter :	2
Z :	3
G name :	G188


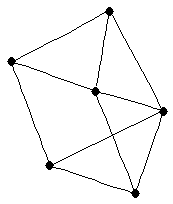
graph6 :	E\|Ug
Order :	6
mr :	2
M :	4
ω :	3
δ :	3
cc :	6
Diameter :	2
Z :	4
G name :	G189


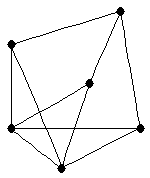
graph6 :	Elto
Order :	6
mr :	2
M :	4
ω :	3
δ :	3
cc :	4
Diameter :	2
Z :	4
G name :	G190


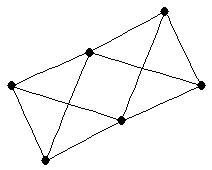
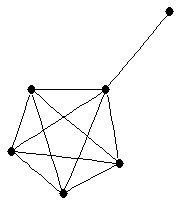
graph6 :	EmvW
Order :	6
mr :	2
M :	4
ω :	5
δ :	1
cc :	2
Diameter :	2
Z :	4
G name :	G191


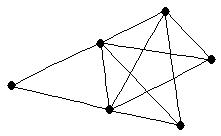
graph6 :	E\|jg
Order :	6
mr :	3
M :	3
ω :	3
δ :	2
cc :	3
Diameter :	2
Z :	3
G name :	G192


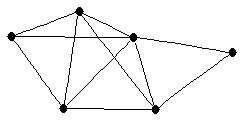
graph6 :	EnfW
Order :	6
mr :	3
M :	3
ω :	4
δ :	2
cc :	3
Diameter :	2
Z :	3
G name :	G193


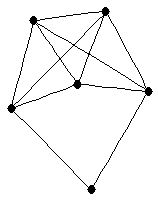
graph6 :	E~]G
Order :	6
mr :	2
M :	4
ω :	4
δ :	2
cc :	4
Diameter :	2
Z :	4
G name :	G194


graph6 :	Ento
Order :	6
mr :	2
M :	4
ω :	4
δ :	3
cc :	2
Diameter :	2
Z :	4
G name :	G195


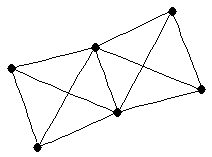graph6 :	Elfw
Order :	6
mr :	3
M :	3
ω :	4
δ :	3
cc :	4
Diameter :	2
Z :	3
G name :	G196


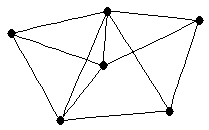graph6 :	Erfw
Order :	6
mr :	2
M :	4
ω :	3
δ :	3
cc :	6
Diameter :	2
Z :	4
G name :	G197


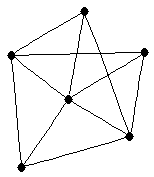graph6 :	Eltw
Order :	6
mr :	3
M :	3
ω :	3
δ :	3
cc :	5
Diameter :	2
Z :	3
G name :	G198


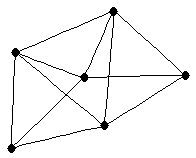graph6 :	Eluw
Order :	6
mr :	2
M :	4
ω :	4
δ :	3
cc :	4
Diameter :	2
Z :	4
G name :	G199


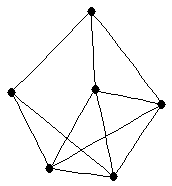graph6 :	E~Fw
Order :	6
mr :	2
M :	4
ω :	5
δ :	2
cc :	2
Diameter :	2
Z :	4
G name :	G200


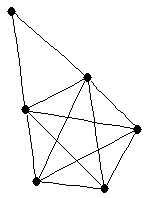graph6 :	E~z_
Order :	6
mr :	2
M :	4
ω :	4
δ :	3
cc :	3
Diameter :	2
Z :	4
G name :	G201


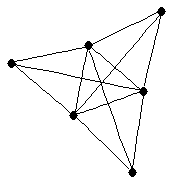graph6 :	E\|ng
Order :	6
mr :	3
M :	3
ω :	4
δ :	3
cc :	3
Diameter :	2
Z :	3
G name :	G202


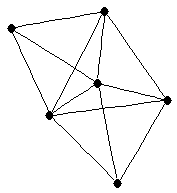graph6 :	Elzw
Order :	6
mr :	2
M :	4
ω :	4
δ :	3
cc :	4
Diameter :	2
Z :	4
G name :	G203

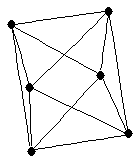
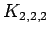$K_{2,2,2}$ complete tripartite graph on 2,2,2-vertices
graph6 :	E\|tw
Order :	6
mr :	2
M :	4
field independent :	yes
ω :	3
δ :	4
cc :	6
Diameter :	2
maxinducedpath :	2
Z :	4
α :	2
G name :	G204
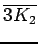
Notes :	4-regular, $\overline{3K_2}$ References: [BvdHL], [BvdHL2]


graph6 :	E\|}w
Order :	6
mr :	2
M :	4
ω :	5
δ :	3
cc :	2
Diameter :	2
Z :	4
G name :	G205

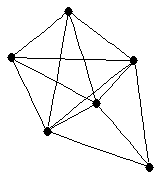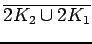
$\overline{2K_2\cup 2K_1}$
graph6 :	E~tw
Order :	6
mr :	2
M :	4
field independent :	yes
ω :	4
δ :	4
cc :	4
Diameter :	2
maxinducedpath :	2
Z :	4
α :	2
G name :	G206
Notes :	References: [BvdHL], [BvdHL2]


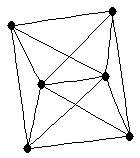graph6 :	E~~o
Order :	6
mr :	2
M :	4
ω :	5
δ :	4
cc :	2
Diameter :	2
Z :	4
G name :	G207

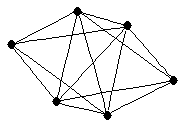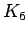complete graph on 6 vertices
graph6 :	E~~w
Order :	6
mr :	1
M :	5
field independent :	yes
ξ :	5
ω :	6
δ :	5
tw :	5
cc :	1
Diameter :	1
maxinducedpath :	1
Z :	5
α :	1
G name :	G208

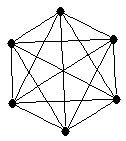4-antiprism
graph6 :	GzK[]K
Order :	8
mr :	4
M :	4
ξ :	4
ω :	3
δ :	4
Z :	4
Notes :	Reference: [AIM]

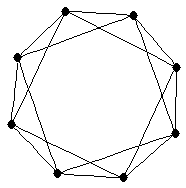Petersen graph
graph6 :	IheA@GUAo
Order :	10
mr :	5
M :	5
ω :	2
δ :	3
cc :	15
Diameter :	2
Z :	5
Notes :	Reference: [AIM] (the picture is misleading - unfortunately an edge lies on top of a vertex it does not intersect)

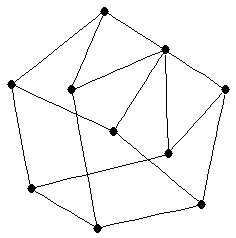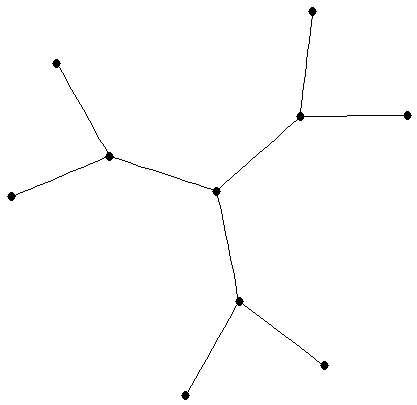
$T_{BF}$ Barioli-Fallat Tree
graph6 :	IXAGGA@?G
Order :	10
mr :	6
M :	4
field independent :	yes
ξ :	2
ω :	2
δ :	1
tw :	1
cc :	9
Diameter :	4
maxinducedpath :	4
Z :	4
α :	7
Notes :	This tree allows ordered multiplicity list 1,2,4,2,1 for certain real numbers and not for others, showing that the determination of ordered multiplicity lists is not equivlanet to solving the Inverse Eigenvalue Problem of a Graph, even for trees. Reference: [BF]

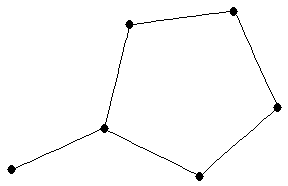
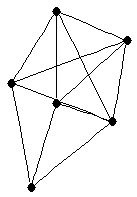
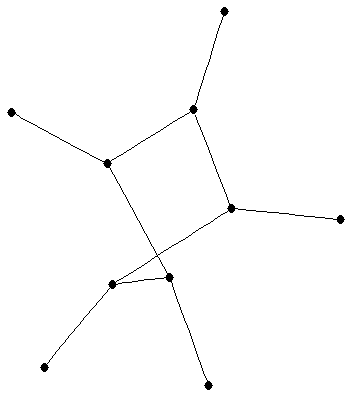
$C_5\circ K_1$ pentasun (corona of 5-cycle with a point)
graph6 :	IheA@?OA?
Order :	10
mr :	8
M :	2
field independent :	yes
ξ :	2
ω :	2
δ :	1
cc :	10
Diameter :	4
maxinducedpath :	5
Z :	3
α :	5
Notes :	First known example 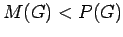where where 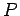is path cover number. References: [BFH04]