
What is a representation?
Symmetry is a fundamental principle of nature, and behind anything symmetric is a mathematical object called a Lie group. Lie groups are ubiquitous, and mathematicians study Lie groups both for their inherent beauty and with applications to other fields in mind.Every Lie group can appear in various guises: these are called representations. More precisely, a representation of a group is a realization of that group inside a group of matrices. For example here is the circle sitting inside 2x2 matrices;
|
Mathematicians would like to understand all representations of E8. The basic building blocks of all representation are irreducible representations; for many purposes it is enough to understand these. There are infinitely many of them. For E8 there is a basic reduction which cuts this down to a finite (but large!) number: 453,060.
There are very precise intricate relationships between these 453,060 representations. This is sometimes referred to as character theory, by analogy with the character table of a finite group. This information is encoded in a matrix of size 453,060, with 205,263,363,600 (205 billion) entries. These are known to mathematicians as Kazhdan-Lusztig-Vogan polynomials. This structure is like the human genome: it contains all of information about character theory of E8, carefully encoded and tightly packaged.
To find this information mathematicians must solve a fantastically complicated set of equations. Part of the challenge was not knowing beforehand the size of the answer (the number of non-zero entries).
Until recently finding this matrix was considered to be impractical, even with the world's most powerful computers. Recent advances in mathematics and computer science have converged and brought this problem to the very edge of what it is possible to compute.
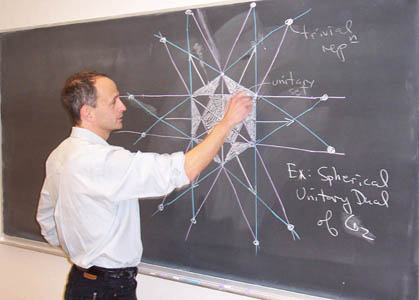
The Lie group G2 is sufficiently simple that some of its representation theory can be described with a picture.
 |