I. Problems suggested by the participants
Thomas Branson. Anti-conformal perturbations.
Problem 1a: Given any functional of the metric that is well understood conformally, is there information that can arise going across conformal classes?
If the functional is the integral of a local invariant we can obtain information by computing its anti-conformal variation. If the functional is a nonlocal spectral invariant, like the functional determinant, then it is even a challenge to compute the anti-conformal deformation.
Problem 1b: How to obtain the information that arises going across conformal classes?
Problem 1c: Study variational problems arising from conformally invariant problems.
Michael Eastwood.
Problem 2: Find an explicit relation between ![]() and
and
![]() in the
conformally flat case.
in the
conformally flat case.
Problem 3: Is there a global ambient metric construction?
Problem 4: Can we explicitly write ![]() in dimension 6
uniquely as constant times
in dimension 6
uniquely as constant times
![]() plus local conformally invariant plus divergence?
plus local conformally invariant plus divergence?
Answer to problem 4: Robin Graham reports the answer to be YES.
Alice Chang. General problems in conformal geometry:
Problem 5a: How to decide which curvature invariants have
a conformal primitive? For
example on manifold ![]() we have
we have
![]() has
has
![]() as a conformal primitive,
i.e.
as a conformal primitive,
i.e.
Problem 5b: What characterizes such curvature invariants?
A related problem is posed by T. Branson:
On ![]() ,
, ![]() curvature is a local invariant (of density weight
curvature is a local invariant (of density weight
![]() )
which does not have a conformal primitive. The local invariants that have
conformal primitives form a vector
subspace, say
)
which does not have a conformal primitive. The local invariants that have
conformal primitives form a vector
subspace, say ![]() of the space of local invariants
of the space of local invariants ![]() Thus the
quotient space
Thus the
quotient space
![]() is the space which
measures ``how many things'' do not have a conformal primitive. There are
also local conformal invariants,
is the space which
measures ``how many things'' do not have a conformal primitive. There are
also local conformal invariants,
![]() say.
say.
Problem 6: Is
![]() one-dimensional and
generated by the class of
one-dimensional and
generated by the class of ![]()
Problem 7: On ![]() , Gursky (``The principal eigenvalue of
a conformally invariant
differential operator, with an application to semilinear elliptic PDE.''
Comm. Math. Phys., 207(1):131-143, 1999.)
proved that if
, Gursky (``The principal eigenvalue of
a conformally invariant
differential operator, with an application to semilinear elliptic PDE.''
Comm. Math. Phys., 207(1):131-143, 1999.)
proved that if ![]() and if
and if ![]() , then the Paneitz operator
, then the Paneitz operator
![]() is positive with its kernel consisting of
constants. The original proof given by Gursky depends on estimates of
solution of some non-linear PDE. Can one also see this fact
from the construction method of the general GJMS operators?
is positive with its kernel consisting of
constants. The original proof given by Gursky depends on estimates of
solution of some non-linear PDE. Can one also see this fact
from the construction method of the general GJMS operators?
Claude LeBrun.
Problem 8: Explicitly expess the
Gauss-Bonnet integrand as a sum of
![]() plus terms
involving the Weyl
curvature, and then use this to explicitly understand relationships
between
plus terms
involving the Weyl
curvature, and then use this to explicitly understand relationships
between ![]() and
topology.
and
topology.
Problem 9: Given a compact manifold of even dimension ![]() show that there exists a sequence of
metrics such that
show that there exists a sequence of
metrics such that
![]() .
.
Robin Graham
Problem 10: If ![]() is even, is there a nonzero
scalar conformal invariant of
weight
is even, is there a nonzero
scalar conformal invariant of
weight ![]() which is expressible as a linear combination of complete
contractions of the tensors
which is expressible as a linear combination of complete
contractions of the tensors
![]() ,
, ![]() ?
?
If the answer to this question is no, then the ![]() -curvature
defined via the ambient
metric construction is uniquely determined by its transformation law in
terms of the GJMS operator
-curvature
defined via the ambient
metric construction is uniquely determined by its transformation law in
terms of the GJMS operator
![]() and the fact that it can be written just in terms of
and the fact that it can be written just in terms of
![]() and its
derivatives. The answer
is no if
and its
derivatives. The answer
is no if ![]() . It is worth pointing out that there are scalar conformal
invariants of more
negative weight which can be so expressed: the norm squared of the Bach
tensor is of this form if
. It is worth pointing out that there are scalar conformal
invariants of more
negative weight which can be so expressed: the norm squared of the Bach
tensor is of this form if
![]() , as is the norm squared of the ambient obstruction tensor in higher
even dimensions.
, as is the norm squared of the ambient obstruction tensor in higher
even dimensions.
Problem 11: If ![]() is even, is the GJMS operator
is even, is the GJMS operator
![]() the only natural
differential operator with principal part
the only natural
differential operator with principal part ![]() whose
coefficients can be expressed
purely in terms of the tensors
whose
coefficients can be expressed
purely in terms of the tensors
![]() ,
, ![]() , and which is
conformally invariant from
, and which is
conformally invariant from
![]() to
to
![]() ?
?
If the answer is yes, then this gives a characterization of the
GJMS operator ![]() .
Combined with a negative answer to Problem 11, this would provide a unique
specification of
.
Combined with a negative answer to Problem 11, this would provide a unique
specification of ![]() .
.
Rod Gover Alice Chang and Jie Qing have an order 3
operator ![]() on 3-manifolds (boundary of a
4-dimensional manifold, or embedded in a 4-dimensional manifold). There
is a version of
on 3-manifolds (boundary of a
4-dimensional manifold, or embedded in a 4-dimensional manifold). There
is a version of ![]() associated to this
associated to this ![]()
Problem 12: What sort of information is encoded by ![]() and/or
and/or ![]()
Helga Baum On a spin manifold ![]() with spin bundle
with spin bundle
![]() we have two conformally
covariant operators. The Dirac operator
we have two conformally
covariant operators. The Dirac operator ![]() and the twistor operator
and the twistor operator
![]() If
If ![]() represents the spin connection then,
represents the spin connection then,
Problem 13: Find all Lorentzian conformal structures
![]() with
with
![]() or
or ![]()
Problem 14: How ![]() and
and ![]() relate to other
conformal
invariants?
relate to other
conformal
invariants?
Problem 15: Relate ![]() to the holonomy of conformal
Cartan
connections.
to the holonomy of conformal
Cartan
connections.
Problem 16: Relate ![]() to the dynamic of null
geodesics.
to the dynamic of null
geodesics.
Problem 17: Describe conformally flat Lorentzian manifolds
with
![]() or
or ![]() .
.
II. Problems extracted from the document ``A Primer on
![]() -curvature'' by M. Eastwood and
J. Slovàck.
1
-curvature'' by M. Eastwood and
J. Slovàck.
1
In the conformally flat case, locally by setting
![]() where
where ![]() is flat, then
is flat, then
Problem 18: Deduce fact 2 from fact 1 or vice versa. Alternatively, construct a Lie algebraic proof of fact 2.
About a formula for ![]() Eastwood and Slováck have deduce:
Eastwood and Slováck have deduce:
It is possible, by further differentiating (![]() ), to obtain
a formula for
), to obtain
a formula for
![]() expressed in terms of complete contractions of
expressed in terms of complete contractions of
![]() ,
its hatted derivatives, and
,
its hatted derivatives, and ![]() . With increasing
. With increasing ![]() , this gets
rapidly out of hand.
Moreover, it is only guaranteed to give
, this gets
rapidly out of hand.
Moreover, it is only guaranteed to give ![]() in the conformally flat case.
Indeed, when
in the conformally flat case.
Indeed, when ![]() this
naive derivation of
this
naive derivation of ![]() fails for a general metric.
fails for a general metric.
Problem 19: Find a formula for ![]() in the conformally flat
case. Show that the
procedure outlined by Eastwood and Slováck produces a formula for
in the conformally flat
case. Show that the
procedure outlined by Eastwood and Slováck produces a formula for ![]() .
.
In the conformally flat case, it follows from a theorem of
Branson, Gilkey, and Pohjanpelto that ![]() must be a multiple of the
Pfaffian
plus a divergence.
must be a multiple of the
Pfaffian
plus a divergence.
Problem 20: Find a direct link between ![]() and the
Pfaffian in the conformally flat
case. Prove directly that
and the
Pfaffian in the conformally flat
case. Prove directly that ![]() is a topological invariant in this
case.
is a topological invariant in this
case.
Problem 21: Is it true that, on a general Riemannian
manifold, ![]() may be written as a
multiple of the Pfaffian plus a local conformal invariant plus a
divergence?
may be written as a
multiple of the Pfaffian plus a local conformal invariant plus a
divergence?
See Problem 4 for the 6
dimensional case. Also, T. Branson has appointed that if it is true that
any local invariant ![]() of
density weight
of
density weight ![]() has the form
has the form
How is ![]() -curvature related to Weyl structures?
-curvature related to Weyl structures? ![]() may
be defined for a Weyl
structure as follows. Since
may
be defined for a Weyl
structure as follows. Since ![]() is a Riemannian invariant, the
differential
operator
is a Riemannian invariant, the
differential
operator ![]() is necessarily of the form
is necessarily of the form
![]() for some
Riemannian invariant linear differential operator from
for some
Riemannian invariant linear differential operator from ![]() -forms to
-forms to
![]() -forms.
Now, if
-forms.
Now, if
![]() is a Weyl structure, choose a representative
metric
is a Weyl structure, choose a representative
metric
![]() and consider the
and consider the ![]() -form
-form
Problem 22: Can we find such a ![]() in general
even dimensions?
Presumably, this would restrict the choice of Riemannian
in general
even dimensions?
Presumably, this would restrict the choice of Riemannian ![]() .
.
Though ![]() is an invariant of the Weyl
structure, it is not manifestly so. With a detailed calculation, Eastwood
and Slov`ack have shown that
in dimension 4:
is an invariant of the Weyl
structure, it is not manifestly so. With a detailed calculation, Eastwood
and Slov`ack have shown that
in dimension 4:
Problem 23: Did we really need to go through that detailed
calculation? What are the
implications, if any, for the operator
![]() ?
?
Problem 24 a: Can we characterise the Riemannian ![]() by
sufficiently many properties?
by
sufficiently many properties?
Problem 24 b: Do Weyl structures help in this regard?
Tom Branson has suggested that, for two metrics ![]() and
and
![]() in the same conformal class on a compact manifold
in the same conformal class on a compact manifold ![]() , one should consider
the
quantity
, one should consider
the
quantity
Problem 25: Are there any deeper properties of Branson's
cocycle
![]() ?
?
One possible rôle for ![]() is in a curvature prescription
problem:
is in a curvature prescription
problem:
Problem 26: On a given manifold ![]() , can one find a metric
with specified
, can one find a metric
with specified ![]() ?
?
One can also ask this question within a given conformal class or
within the
realm of conformally flat metrics though, of course, if ![]() is compact,
then
is compact,
then
![]() must be as specified by the conformal class and the topology
of
must be as specified by the conformal class and the topology
of ![]() .
.
Problem 27: When does ![]() determine the metric up to
constant rescaling within a given
conformal class?
determine the metric up to
constant rescaling within a given
conformal class?
Since we know how ![]() changes under conformal rescaling:
changes under conformal rescaling:
Problem 28: When does the equation ![]() have only
constant solutions?
have only
constant solutions?
On a compact manifold in two dimensions this is always true:
harmonic functions
are constant. In four dimensions, though there are conditions under which
![]() has only constant solutions, there are also counterexamples, even
on
conformally flat manifolds.
has only constant solutions, there are also counterexamples, even
on
conformally flat manifolds.
III. Problems extracted from the document ``Origins,
applications, and generalizations of
the ![]() -curvature'' by T. Branson and R. Gover.
2
-curvature'' by T. Branson and R. Gover.
2
Let ![]() be a natural differential operator with positive
definite
leading symbol, and suppose
be a natural differential operator with positive
definite
leading symbol, and suppose ![]() is a positive power of a conformally
invariant operator. For example,
is a positive power of a conformally
invariant operator. For example, ![]() could be one of the GJMS
operators, or it could be the square of the Dirac operator.
Then in dimensions 2,4,6,
could be one of the GJMS
operators, or it could be the square of the Dirac operator.
Then in dimensions 2,4,6,
Problem 29:
3Is (![]() ) true in higher even dimensions?
) true in higher even dimensions?
The following conjecture would be enough to answer the previous problem.
Problem 30: If ![]() is a natural
is a natural ![]() -form and
-form and
![]() is
conformally invariant, then
is
conformally invariant, then
Problem 31: Is it possible to write any ![]() as in
Problem 30, in the form
as in
Problem 30, in the form
Problem 32: Is it possible to write any ![]() as in
Problem 30, in the form
as in
Problem 30, in the form
Other routes to ![]() There is an alternative definition of
There is an alternative definition of
![]() which avoids dimensional
continuation. Let
which avoids dimensional
continuation. Let ![]() be the space of smooth functions, let
be the space of smooth functions, let
![]() be space of smooth
1-forms and define the special section
be space of smooth
1-forms and define the special section
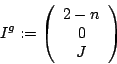
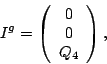
![\begin{displaymath}
\nabla_a \left(\begin{array}{c} \sigma \\ \mu \\ \tau \end{a...
...ebox[0.4em][l]{\tiny $\vert$}}{\mbox{\sf P}}\end{array}\right)
\end{displaymath}](img125.gif)
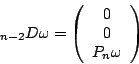
While this definition avoids dimensional continuation, there is
still the issue of
getting a formula for ![]() . There is an effective algorithm for
re-expressing the ambient results in terms of tractors which then
expand easily into formulae in terms of the underlying Riemannian
curvature and its covariant derivatives, solving the problem for small
. There is an effective algorithm for
re-expressing the ambient results in terms of tractors which then
expand easily into formulae in terms of the underlying Riemannian
curvature and its covariant derivatives, solving the problem for small
![]() .
.
Problem 33: Give general formulae or inductive formulae
for the operators ![]() .
.
In another direction there is
another exercise to which already are some answers. One of the
features of the ![]() -curvature is that it ``transforms by a linear
operator''
within a conformal class.
More precisely, it is an example of a natural Riemannian tensor-density
field
with a transformation law
-curvature is that it ``transforms by a linear
operator''
within a conformal class.
More precisely, it is an example of a natural Riemannian tensor-density
field
with a transformation law
Problem 34: Construct other natural tensor-densities which
transform according
to (![]() ). (Note that any solution yields a conformally invariant
natural operator
). (Note that any solution yields a conformally invariant
natural operator ![]() .)
.)
Solutions to Problem 34 have a role to play in the problem of
characterizing the
![]() -curvature and the GJMS operators.
-curvature and the GJMS operators.
Generalizations of ![]() In a compact, oriented, but not necessarily connected, manifold of even
dimension
In a compact, oriented, but not necessarily connected, manifold of even
dimension ![]()
![]() can be seen as a multiplication operator from the closed 0-forms
can be seen as a multiplication operator from the closed 0-forms
![]() (i.e. the locally constant functions) into the space of
(i.e. the locally constant functions) into the space of ![]() -forms
-forms
![]() (identified with
(identified with
![]() via the conformal Hodge
via the conformal Hodge ![]() ). This
operator has the following
properties:
). This
operator has the following
properties:
The idea now is to look for analogous operators on other forms.
T. Branson and R. Gover (see math.DG/0309085) have used the
ambient metric, and its relationship to tractors,
to show that the previous generalizes along the following lines:
There are operators
![]() (
(![]() ),
given by a uniform construction, with the following properties:
),
given by a uniform construction, with the following properties:
Problem 35: There are analogues for the operators ![]() of most of the Problems in Sections II. and III. for the
of most of the Problems in Sections II. and III. for the ![]() -curvature.
-curvature.
Back to the
main index
for Conformal structure in Geometry, Analysis, and Physics .