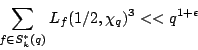Mean-values
There are so many results and conjectures having to do with the mean-values
or moments of L-functions in families that it is difficult to mention
all of them. So we will stick with some of the more familiar ones.
Moments of 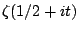 . Let
. Let
Then asymptotic formulae are known for 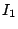 and
and 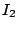 . A good estimation for
. A good estimation for 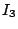 seems to be far out of reach of today's technology (maybe we need to know
more about automorphic forms on GL3?) but would be a very important milestone. Conjectures based on number theory are known for
seems to be far out of reach of today's technology (maybe we need to know
more about automorphic forms on GL3?) but would be a very important milestone. Conjectures based on number theory are known for 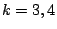 . Conjectures based on random matrix theory are known for all real
. Conjectures based on random matrix theory are known for all real 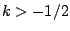 .
.
Moments of 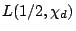 . Let
. Let 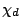 be a real, primitive, quadratic character to the modulus
be a real, primitive, quadratic character to the modulus 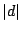 (i.e. a Kronecker symbol).
Let
(i.e. a Kronecker symbol).
Let
Then asymptotics are known for 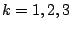 . A conjecture based on number theory is known for
. A conjecture based on number theory is known for 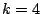 . Conjectures based on random matrix theory are known for all real
. Conjectures based on random matrix theory are known for all real 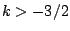 . The fourth moment is just slightly out of reach of current technology.
. The fourth moment is just slightly out of reach of current technology.
Moments of automorphic L-functions. Let 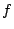 be a normalized newform of weight
be a normalized newform of weight 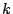 and level 1 and let
and level 1 and let 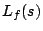 be the associated
be the associated 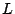 -function
(with critical strip
-function
(with critical strip 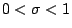 .) Let
.) Let
Then asymptotic formulae are known for
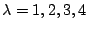 . Conjectures based on random matrix theory are known for all real
. Conjectures based on random matrix theory are known for all real
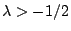 .
Is the fifth moment doable?
.
Is the fifth moment doable?
Quadratic twists of automorphic L-functions. Let 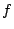 be a fixed newform (for example the newform associated with a given elliptic curve).
Let
be a fixed newform (for example the newform associated with a given elliptic curve).
Let 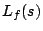 be the associated L-function and
be the associated L-function and 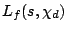 the twist by the primitive quadratic character
the twist by the primitive quadratic character 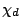 . It is possible to evaluate the
first moment
. It is possible to evaluate the
first moment
but can one do the second moment
Again, this is just at the edge of what can be done by today's techniques
and is a problem worthy of study.
Special families. Recently the bound
has been obtained, where 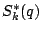 denotes the set of newforms of
weight
denotes the set of newforms of
weight 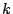 and level
and level 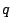 (no character), and
(no character), and 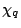 is the real character to the modulus
is the real character to the modulus 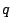 where
where 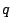 is odd and squarefree. This estimate has been used to bound fourier coefficients of half-integral weight forms and (its analogue for Maass forms has been used) to bound
is odd and squarefree. This estimate has been used to bound fourier coefficients of half-integral weight forms and (its analogue for Maass forms has been used) to bound
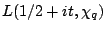 . Can one strengthen this estimate to give
an asymptotic formula (perhaps for
. Can one strengthen this estimate to give
an asymptotic formula (perhaps for 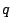 restricted to prime values)? Are there other situations where the underlying arithmetic is so fortuitous so as to give such a strong bound?
restricted to prime values)? Are there other situations where the underlying arithmetic is so fortuitous so as to give such a strong bound?
Back to the
main index
for L-functions and Random Matrix Theory.
![]() . Let
. Let
![]() . Let
. Let ![]() be a real, primitive, quadratic character to the modulus
be a real, primitive, quadratic character to the modulus ![]() (i.e. a Kronecker symbol).
Let
(i.e. a Kronecker symbol).
Let
![]() be a normalized newform of weight
be a normalized newform of weight ![]() and level 1 and let
and level 1 and let ![]() be the associated
be the associated ![]() -function
(with critical strip
-function
(with critical strip ![]() .) Let
.) Let
![]() be a fixed newform (for example the newform associated with a given elliptic curve).
Let
be a fixed newform (for example the newform associated with a given elliptic curve).
Let ![]() be the associated L-function and
be the associated L-function and ![]() the twist by the primitive quadratic character
the twist by the primitive quadratic character ![]() . It is possible to evaluate the
first moment
. It is possible to evaluate the
first moment