A Frobenius manifold is a manifold
 equipped with a smoothly (or analytically) varying structure of a
Frobenius algebra on each tangent space which satisfies a series of
integrability conditions (e.g. the induced metric is required to be
flat). The most relevant example arises in Gromov-Witten theory where
the genus 0 theory of a variety
equipped with a smoothly (or analytically) varying structure of a
Frobenius algebra on each tangent space which satisfies a series of
integrability conditions (e.g. the induced metric is required to be
flat). The most relevant example arises in Gromov-Witten theory where
the genus 0 theory of a variety  imposes a Frobenius manifold
structure on
imposes a Frobenius manifold
structure on
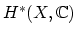 (more precisely, the structure
of a formal, graded-commutative Frobenius manifold). The
integrability condition in this case is equivalent to the
associativity of the quantum product. Other examples arise in the
deformation theory of isolated singularities and in Hodge theory.
(more precisely, the structure
of a formal, graded-commutative Frobenius manifold). The
integrability condition in this case is equivalent to the
associativity of the quantum product. Other examples arise in the
deformation theory of isolated singularities and in Hodge theory.
Jeffrey Herschel Giansiracusa
2005-05-17