Given a topological monoid  , the group completion is the space
, the group completion is the space
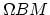 , where
, where 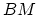 is the classifying space of
is the classifying space of  (thinking of
(thinking of
 as a topological category). If
as a topological category). If  is already a topological
group, then this operation does not change
is already a topological
group, then this operation does not change  up to homotopy
equivalence. Under some assumptions, we have the following
description of the homology of the group completion. If we treat the
monoid
up to homotopy
equivalence. Under some assumptions, we have the following
description of the homology of the group completion. If we treat the
monoid
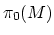 as a directed system (with maps given by the
monoid operation), then
in situations where the direct limit on the left-hand side is
well-defined. In particular, if we consider the monoid
as a directed system (with maps given by the
monoid operation), then
in situations where the direct limit on the left-hand side is
well-defined. In particular, if we consider the monoid
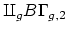 , the homology of the group completion is precisely the
stable homology. The plus construction can often be used to give an
alternative construction of the group completion.
, the homology of the group completion is precisely the
stable homology. The plus construction can often be used to give an
alternative construction of the group completion.
Jeffrey Herschel Giansiracusa
2005-05-17