Harer stability states that the degree  homology of the mapping
class group
homology of the mapping
class group
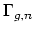 is independent of
is independent of  and
and  if
if  is
small compared to
is
small compared to  . More precisely, consider the following maps on
classifying spaces. First, we construct a map
. More precisely, consider the following maps on
classifying spaces. First, we construct a map
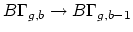 by adjoining a disk to a given boundary
component. Second, we can construct a map
by adjoining a disk to a given boundary
component. Second, we can construct a map
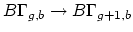 by gluing a torus with two boundary components along
a given boundary component of our original Riemann surface. Harer's
stability theorem asserts that both of these maps induce an
isomorphism on
by gluing a torus with two boundary components along
a given boundary component of our original Riemann surface. Harer's
stability theorem asserts that both of these maps induce an
isomorphism on
 for
for 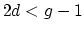 . In particular,
it allows us to talk about the stable homology/cohomology of the
moduli space of curves, as in Mumford's conjecture.
. In particular,
it allows us to talk about the stable homology/cohomology of the
moduli space of curves, as in Mumford's conjecture.
Jeffrey Herschel Giansiracusa
2005-05-17