Given a category 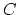 , its nerve
, its nerve 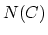 is the simplicial set
constructed as follows. The set
is the simplicial set
constructed as follows. The set 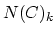 of
of 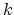 -simplices is the
set of diagrams
of objects and morphisms from
-simplices is the
set of diagrams
of objects and morphisms from 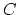 . The face maps
. The face maps
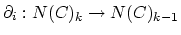 are given by composition of morphisms atthe
are given by composition of morphisms atthe
 node in the diagram (or dropping the first or last arrow if
node in the diagram (or dropping the first or last arrow if
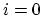 or
or 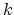 respectively), and the degeneracy maps are given by
inserting identity morphisms. The intuition here is that a
respectively), and the degeneracy maps are given by
inserting identity morphisms. The intuition here is that a
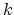 -simplex in
-simplex in 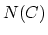 is precisely a commutative diagram in
is precisely a commutative diagram in 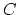 with
the shape of a
with
the shape of a 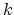 -simplex. If
-simplex. If 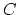 is a topological category, we can
enrich
is a topological category, we can
enrich 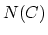 to be a simplicial space.
to be a simplicial space.
Jeffrey Herschel Giansiracusa
2005-05-17