The classifying space 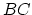 of a category
of a category 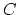 is the geometric
realization of the nerve
is the geometric
realization of the nerve 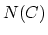 . That is,
where the
equivalence relation
. That is,
where the
equivalence relation 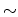 glues the
glues the 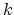 -simplices togetehr as
specified by the face and degeneracy maps of
-simplices togetehr as
specified by the face and degeneracy maps of 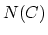 . For a group
. For a group  ,
we can consider the category with a single object and morphisms given
by elements of
,
we can consider the category with a single object and morphisms given
by elements of  ; in this case, this construction recovers the Borel
construction
; in this case, this construction recovers the Borel
construction 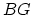 . More generally, given a group
. More generally, given a group  acting on a
space
acting on a
space  , we can construct a (topological) category whose objects are
given by points in
, we can construct a (topological) category whose objects are
given by points in  and whose morphisms are given by elements of
and whose morphisms are given by elements of
 . The classifying space of this category is the homotopy quotient
. The classifying space of this category is the homotopy quotient
 . If
. If 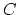 is a strict symmetric monoidal
category then
is a strict symmetric monoidal
category then 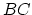 will be an infinite loop space.
will be an infinite loop space.
Note that in algebraic geometry, ``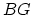 '' often refers to the stack-theoretic
quotient
'' often refers to the stack-theoretic
quotient
![$ [\mathrm{point} / G]$](img38.png) .
.
Jeffrey Herschel Giansiracusa
2005-05-17
![]() '' often refers to the stack-theoretic
quotient
'' often refers to the stack-theoretic
quotient
![]() .
.