The Virasoro conjecture is a
series of relations among the full Gromov-Witten invariants of a
smooth projective variety  for all genera. If one encodes all
Gromov-Witten invariants (including descendents) in a generating
function
for all genera. If one encodes all
Gromov-Witten invariants (including descendents) in a generating
function 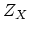 , these relations are expressed as a sequence of
differential operators
, these relations are expressed as a sequence of
differential operators 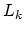 (for
(for 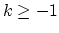 ) for which
and
That is, these operators give a
representation of half of the Virasoro algebra of differential
operators
) for which
and
That is, these operators give a
representation of half of the Virasoro algebra of differential
operators
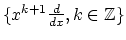 on
on  . The
conjecture is currently known for toric Fano varieties and for curves
(as well as some other trivial cases). One strange feature of the
Virasoro relations is that their definition relies upon the Hodge
decomposition in a weak but nontrivial way. In particular, they are
not defined for arbitrary symplectic manifolds, even though
Gromov-Witten invariants are defined in this context.
. The
conjecture is currently known for toric Fano varieties and for curves
(as well as some other trivial cases). One strange feature of the
Virasoro relations is that their definition relies upon the Hodge
decomposition in a weak but nontrivial way. In particular, they are
not defined for arbitrary symplectic manifolds, even though
Gromov-Witten invariants are defined in this context.
Jeffrey Herschel Giansiracusa
2005-05-17