There are  natural line bundles
natural line bundles  over
over
 (or
(or
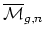 ); the fibre at
); the fibre at 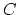 of
of  is the
cotangent space
is the
cotangent space
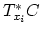 , where
, where 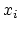 is the
is the  marked point
in
marked point
in 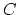 . The Witten class
. The Witten class 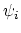 is then the first Chern class of
is then the first Chern class of
 . These live naturally in the cohomology of either the
compactified or non-compactified moduli space.
. These live naturally in the cohomology of either the
compactified or non-compactified moduli space.
Jeffrey Herschel Giansiracusa
2005-05-17