These are
operations on the mod- homology of infinite loop spaces. They
measure the failure of the Pontrjagin product to be commutative at the
chain-level and are analogous to the Steenrod squares.
The operations are linear maps of the form
for
homology of infinite loop spaces. They
measure the failure of the Pontrjagin product to be commutative at the
chain-level and are analogous to the Steenrod squares.
The operations are linear maps of the form
for
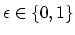 and
and
 .
.
Jeffrey Herschel Giansiracusa
2005-05-17