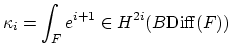Given a genus 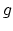 surface
surface 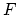 , consider the
universal
, consider the
universal 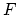 -bundle
-bundle 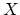 over
over
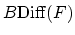 and let
and let 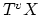 be
its vertical tangent bundle with Euler class
be
its vertical tangent bundle with Euler class
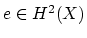 . We
define cohomology classes
. We
define cohomology classes
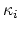 on
on
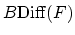 by
where
by
where
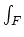 denotes the Gysin push-forward map (i.e. integration over
the fiber). Mumford's conjecture states that these classes freely
generate the stable cohomology ring of the mapping class group. A
natural extension of these classes to the Deligne-Mumford compactified
moduli space was given by Arbarello and Cornalba.
denotes the Gysin push-forward map (i.e. integration over
the fiber). Mumford's conjecture states that these classes freely
generate the stable cohomology ring of the mapping class group. A
natural extension of these classes to the Deligne-Mumford compactified
moduli space was given by Arbarello and Cornalba.
Jeffrey Herschel Giansiracusa
2005-06-27