Let 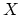 be a space and
be a space and
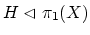 a normal subgroup
that is perfect (i.e.
a normal subgroup
that is perfect (i.e. ![$ [H,H] = H$](img135.png) ). The plus construction is the
essentially unique space
). The plus construction is the
essentially unique space 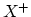 with fundamental group
with fundamental group
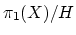 and equipped with a map
and equipped with a map
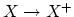 which induces an
isomorphism on homology for all coefficients. It is useful in
situations where one is given a map
which induces an
isomorphism on homology for all coefficients. It is useful in
situations where one is given a map
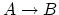 which is an
isomorphism on homology groups but acts wildly on homotopy groups; in
some situations, applying the plus construction can replace this
homology equivalence with a homotopy equivalence--this is how the
plus construction plays a role in group completion.
which is an
isomorphism on homology groups but acts wildly on homotopy groups; in
some situations, applying the plus construction can replace this
homology equivalence with a homotopy equivalence--this is how the
plus construction plays a role in group completion.
Jeffrey Herschel Giansiracusa
2005-06-27