The boundary of
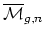 is the
complement of the open subset
is the
complement of the open subset
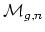 . It is of pure (complex)
codimension 1. It consists of irreducible components
. It is of pure (complex)
codimension 1. It consists of irreducible components
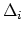 ,
,
![$ i= 0, \dots, [g/2]$](img20.png) where a generic curve in
where a generic curve in
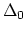 is a
(geometric) genus
is a
(geometric) genus 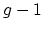 curve with a single node and a generic curve
in
curve with a single node and a generic curve
in
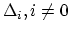 consists of a genus
consists of a genus 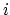 curve attached to a
genus
curve attached to a
genus 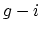 curve at a single node. Each boundary divisor is a
finite-group quotient of a product of
curve at a single node. Each boundary divisor is a
finite-group quotient of a product of
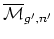 's for
's for 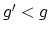 and
and
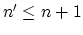 . The subspace
. The subspace
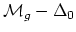 is called the locus of
curves of compact type.
is called the locus of
curves of compact type.
Jeffrey Herschel Giansiracusa
2005-06-27