A spectrum
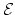 is (roughly) a
sequence of based spaces
is (roughly) a
sequence of based spaces
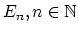 , provided with maps
, provided with maps
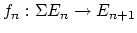 (where
(where 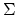 denotes
suspension). There are many different definitions of the category of
spectra, but they all yield the same homotopy category, known as the
stable homotopy category. The homotopy category of spectra forms
a triangulated category (with shifts given by suspension and looping);
if we associate to a space
denotes
suspension). There are many different definitions of the category of
spectra, but they all yield the same homotopy category, known as the
stable homotopy category. The homotopy category of spectra forms
a triangulated category (with shifts given by suspension and looping);
if we associate to a space 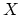 the suspesion spectrum
the suspesion spectrum
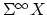 with
with 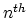 -space
-space
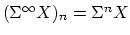 , the homotopy classes of maps between the suspension
spectra of
, the homotopy classes of maps between the suspension
spectra of 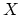 and
and 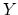 are the stable homotopy classes of maps between
are the stable homotopy classes of maps between
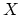 and
and 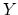 . There is a correspondence between generalized
(co)homology theories and spectra as follows. Given a generalized
cohomology theory
. There is a correspondence between generalized
(co)homology theories and spectra as follows. Given a generalized
cohomology theory 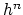 , the Brown representability theorem gives a
(universal) space
, the Brown representability theorem gives a
(universal) space 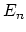 such that
such that
![$ h^{n}(X) = [X,E_{n}]$](img166.png) ; the
suspension axiom provides the required structure maps for
; the
suspension axiom provides the required structure maps for 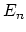 to
form a spectrum. Conversely, for any spectrum
to
form a spectrum. Conversely, for any spectrum
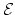 , the
functor
, the
functor
![$ h^n(X) = [X,\Omega^n \mathcal{E}]$](img167.png) is a generalized
cohomology theory, and
is a generalized
cohomology theory, and
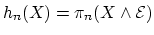 is a
generalized homology theory.
is a
generalized homology theory.
Jeffrey Herschel Giansiracusa
2005-06-27