A variety 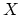 is unirational if
there is a map
is unirational if
there is a map
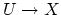 from an open subset
from an open subset
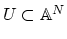 of some affine space whose image contains a dense,
open subset of
of some affine space whose image contains a dense,
open subset of 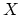 . For instance,
. For instance,
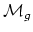 is unirational means that
there is a family of curves on an open subset of affine space which
contains a general curve of genus
is unirational means that
there is a family of curves on an open subset of affine space which
contains a general curve of genus 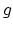 . This is known to be the case
for
. This is known to be the case
for  . Moreover, since unirational implies Kodaira
dimension
. Moreover, since unirational implies Kodaira
dimension 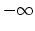 , the result of Eisenbud, Harris, and Mumford shows
that
, the result of Eisenbud, Harris, and Mumford shows
that
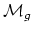 is not unirational for
is not unirational for 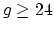 .
.
Jeffrey Herschel Giansiracusa
2005-06-27