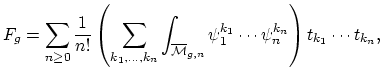Witten's conjecture is a
recursive constraint for top intersections of 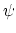 -classes on
-classes on
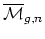 . More precisely, if one considers the generating function
Setting
. More precisely, if one considers the generating function
Setting
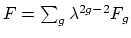 , Witten's conjecture is that
, Witten's conjecture is that
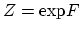 is annihilated by a certain partial differential
operator that also arises in studying the KdV equation in soliton
theory. It can be restated as a specialization of the Virasoro
conjecture for the case where
is annihilated by a certain partial differential
operator that also arises in studying the KdV equation in soliton
theory. It can be restated as a specialization of the Virasoro
conjecture for the case where 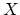 is a point.
is a point.
Multiple proofs of this conjecture now exist, due to Kontsevich,
Okounkov-Pandharipande, and most recently Mirzakhani.
Jeffrey Herschel Giansiracusa
2005-06-27