This document was produced as part of the activities during the
Topology and Geometry of the Moduli space of Curves workshop in March
2005; it is a component of a larger resource site at
http://www.aimath.org/WWN/modspacecurves/
This document originated as a rough transcription of the problems and
questions generated during a discussion session towards the close of
the workshop. Hopefully it will continue to evolve into a repository
of new questions about the moduli space of curves. Towards this goal,
readers are encouraged to submit new questions and information
regarding developments on the questions listed here.
- (Vakil, speaking for Looijenga) Define:
(see compact type
for
definitions of the partial compactifications referred to in the final
three entries above.)
Question: Is it true that
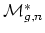 has the homotopy type of a
complex of (real) dimension
has the homotopy type of a
complex of (real) dimension
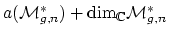 ? If not, is the cohomological dimension
? If not, is the cohomological dimension
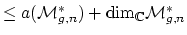 ? What about
quasicoherent cohomological dimension
? What about
quasicoherent cohomological dimension
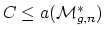 ? Or with
cohomology of
? Or with
cohomology of 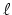 -adic sheaves, is the cohomological dimension
-adic sheaves, is the cohomological dimension
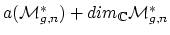 ? (Note that some of these
have already been answered by Looijenga.)
? (Note that some of these
have already been answered by Looijenga.)
These questions come from a master conjecture:
-
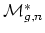 can be covered by fewer than
can be covered by fewer than
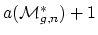 affine varieties.
affine varieties.
- (slightly weaker) It can be stratified by affine
varieties of codimension
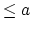 .
.
Here 1a implies 1b, which implies everything else above.
Prof. Looijenga adds the following comment:
It should be mentioned here that Harer (Invent. Math. 84 (1986), 157-176)
proved that
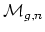 has the homotopy type of a
finite cell complex of dimension
has the homotopy type of a
finite cell complex of dimension 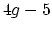 when
when
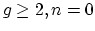 and
and 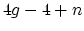 when
when
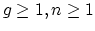 (this answers part of the first question).
I would state my conjecture (in characteristic zero) not just for
(this answers part of the first question).
I would state my conjecture (in characteristic zero) not just for 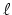 -adic
sheaves, but for all constructible sheaves.
-adic
sheaves, but for all constructible sheaves.
See [HL97] for the source of this series of questions,
and [RV04] for more discussion.
- (Sullivan) Find an explicit cell decomposition of
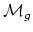 (no
marked points). Sullivan points out that there is no
known cell decomposition of
(no
marked points). Sullivan points out that there is no
known cell decomposition of
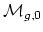 . It was suggested at the problem session
that there may exist a Morse function which would provide such a decomposition.
Looijenga adds the following
remark via email:
My `suspicion' about the existence of a good Morse function on
. It was suggested at the problem session
that there may exist a Morse function which would provide such a decomposition.
Looijenga adds the following
remark via email:
My `suspicion' about the existence of a good Morse function on
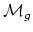 is a bit more
specific and does not involve lengths of geodesics a priori. Rather, it
is related to the set of conjectures mentioned in Problem (1):
it is my hope that there is a naturally defined real-analytic function
is a bit more
specific and does not involve lengths of geodesics a priori. Rather, it
is related to the set of conjectures mentioned in Problem (1):
it is my hope that there is a naturally defined real-analytic function
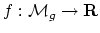 (resp.
(resp.
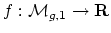 ) which is (a)
bounded from below, (b) proper and (c) is such that its Leviform
) which is (a)
bounded from below, (b) proper and (c) is such that its Leviform
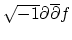 has everywhere at most
has everywhere at most 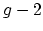 (resp.
(resp. 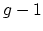 )
eigenvalues
)
eigenvalues 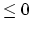 . This would not only imply Harer's result cited
above, but would also imply that the cohomological dimension for
coherent complex-analytic sheaves is at most
. This would not only imply Harer's result cited
above, but would also imply that the cohomological dimension for
coherent complex-analytic sheaves is at most 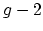 (resp.
(resp. 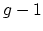 )
and for constructible sheaves is at most
)
and for constructible sheaves is at most
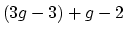 (resp.
(resp.
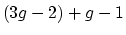 ).
).
In addition, Sarnak has conjectured that
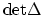 gives a
Morse function on
gives a
Morse function on
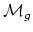 . (Is there a reason for Sarnak to believe
this conjecture true?)
. (Is there a reason for Sarnak to believe
this conjecture true?)
- (Bodigheimer) A question related to both of the previous
problems: What is the Lusternik-Schnirelman category of
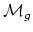 ?
This is a number, bounded above by the dimension, and bounded below
by the cup-length of the cohomology ring (the largest number
of elements in positive degree which have a non-zero cup product.
Can anyone compute the cup-length of the moduli space?
?
This is a number, bounded above by the dimension, and bounded below
by the cup-length of the cohomology ring (the largest number
of elements in positive degree which have a non-zero cup product.
Can anyone compute the cup-length of the moduli space?
- (Getzler et al.) Consider the Hochschild cohomology of the
Fukaya category of a compact Kahler manifold
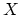 . (Roughly
speaking, the Fukaya category has Lagrangian subspaces as objects
and intersections as morphisms.)
. (Roughly
speaking, the Fukaya category has Lagrangian subspaces as objects
and intersections as morphisms.)
- Is this (naturally) isomorphic to quantum cohomology? The
problem here is to make the known map mathematically rigorous.
What does this have to do with what we know about
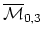 ?
?
- Is the cyclic homology of the Fukaya category of
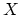 isomorphic
to the Gromow-Witten theory of
isomorphic
to the Gromow-Witten theory of 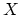 ?
?
Costello's theorems imply that these conjectures are plausible.
Costello comments that the existence of the map should be a purely
analytic question.
- (Bertram) Are there any stable torsion classes
in
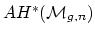 ? (Here
? (Here 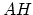 denotes the image of Chow in
cohomology.)
denotes the image of Chow in
cohomology.)
(Mondello) Is there a stable torsion class represented by some
algebraic cycle which geometers "can see"? e.g.
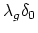 on
on
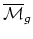 satisfies
satisfies
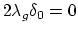 . Is it zero?
Faber says yes, over a field of characteristic 2. Teleman suggests
that there are lots of natural torsion classes in
. Is it zero?
Faber says yes, over a field of characteristic 2. Teleman suggests
that there are lots of natural torsion classes in 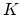 -theory
(arising from the Grotherdieck-Riemann-Roch theorem); how do they
look in cohomology? (Compare to 13 below.)
-theory
(arising from the Grotherdieck-Riemann-Roch theorem); how do they
look in cohomology? (Compare to 13 below.)
(Looijenga) As a related question, it is known that the 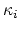 's
live on
's
live on
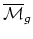 . It is true that all of the stable classes
(so including torsion) live on the orbifold
. It is true that all of the stable classes
(so including torsion) live on the orbifold
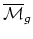 ?
?
- (Madsen) Consider the Torelli group
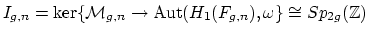 . It is known that the odd classes
. It is known that the odd classes
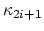 on
on
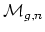 can be pulled back from classes in
can be pulled back from classes in
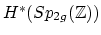 , but the even classes
, but the even classes
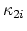 do not come
from the symplectic group. One might thus expect that the even classes pull
back to nontrivial classes on the Torelli group, but surprisingly the answer
is not known. Do the
do not come
from the symplectic group. One might thus expect that the even classes pull
back to nontrivial classes on the Torelli group, but surprisingly the answer
is not known. Do the
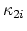 restrict to zero on
restrict to zero on
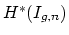 ? Is
this true stably as
? Is
this true stably as
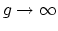 ? Igusa thinks that the answer is
``yes.''
? Igusa thinks that the answer is
``yes.''
- (Madsen) There is a potentially interesting connection between
outer automorphisms and mapping class groups. Let
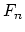 denote the
free group on
denote the
free group on 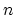 generators and
generators and
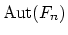 its
automorphism group.
its
automorphism group.
Conjecture:
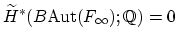 .
.
Daniel Biss (of Chicago) has suggested that the diagram
becomes homotopy cartesian after localization at
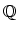 .
Borel's computation of
.
Borel's computation of
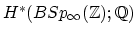 and
and
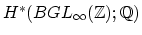 in conjunction with the
Madsen-Weiss calculation of
in conjunction with the
Madsen-Weiss calculation of
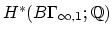 implies the conjecture. Perhaps it might be better to replace
implies the conjecture. Perhaps it might be better to replace
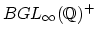 by Waldhausen's
by Waldhausen's 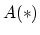 and
and
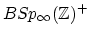 with a symplectic analogue
with a symplectic analogue 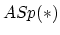 .
(Note:
.
(Note: 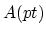 is rationally equivalent to
is rationally equivalent to
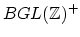 , and
, and
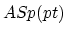 is rationally equivalent to
is rationally equivalent to
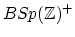 .) The
resulting diagram might then be homotopy cartesian even before
localizing at
.) The
resulting diagram might then be homotopy cartesian even before
localizing at
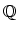 . (We have seen cohomology classes in
. (We have seen cohomology classes in
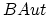 , but they all vanish as rank goes to infinity.)
, but they all vanish as rank goes to infinity.)
Some related thoughts:
What is the relation with the restriction of
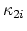 to
to
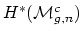 ? Is
? Is
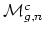 a
a 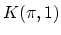 ? Is it true that
? Is it true that
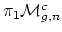 is precisely the kernel of the Johnson homomorphism? Looijenga
points out that the answer to these last two questions is definitely no for large genus. By work of Johnson, the
is precisely the kernel of the Johnson homomorphism? Looijenga
points out that the answer to these last two questions is definitely no for large genus. By work of Johnson, the
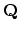 -cohomological dimension
of the (orbifold) fundamental group of
-cohomological dimension
of the (orbifold) fundamental group of
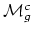 grows like a cubic
polynomial in
grows like a cubic
polynomial in 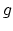 which is certainly larger than the dimension of the space
itself. Instead he proposes the following question.
which is certainly larger than the dimension of the space
itself. Instead he proposes the following question.
- (Looijenga) It is well-known that the map
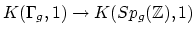 is realized in algebraic geometry as the
period map
is realized in algebraic geometry as the
period map
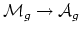 . This map extends to a proper map
. This map extends to a proper map
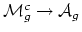 . The former is injective, but the latter
is not (the image of a stable curve of compact type only allows us
to recover its irreducible components of positive genus). Perhaps
less known is the fact that the Eilenberg-MacLane functor applied to
the Johnson truncation
. The former is injective, but the latter
is not (the image of a stable curve of compact type only allows us
to recover its irreducible components of positive genus). Perhaps
less known is the fact that the Eilenberg-MacLane functor applied to
the Johnson truncation
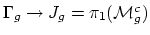 has an
algebro-geometric incarnation as well, namely a lift of the period
map to a torus bundle
has an
algebro-geometric incarnation as well, namely a lift of the period
map to a torus bundle
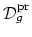 over
over
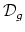 ,
which was studied in depth by Hain. This map also extends to a
proper map
,
which was studied in depth by Hain. This map also extends to a
proper map
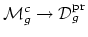 (Theorem 8.6. of
[HL97]). That extension still fails to be injective
in general, but it certainly remembers more that the period map:
given a stable curve
(Theorem 8.6. of
[HL97]). That extension still fails to be injective
in general, but it certainly remembers more that the period map:
given a stable curve 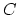 of compact type, then its image in
of compact type, then its image in
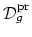 allows us to reconstruct the curve obtained from
allows us to reconstruct the curve obtained from
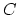 by contracting all of its rational components (so we not only
know its irreducible components of positive genus, but also how they
are connected with each other). Let
by contracting all of its rational components (so we not only
know its irreducible components of positive genus, but also how they
are connected with each other). Let
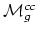 be the
corresponding quotient of
be the
corresponding quotient of
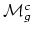 so that we now have a closed
injection
so that we now have a closed
injection
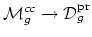 (in the orbifold sense).
(in the orbifold sense).
Question: is this map highly connected in the sense is that orbifold universal cover of
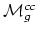 is
is 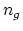 -connected with
-connected with
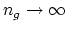 as
as
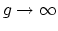 ?
?
Remarks: (a) It is known that the image of the stable cohomology of 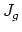 in the rational cohomology of
in the rational cohomology of 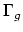 is the subalgebra generated by the
is the subalgebra generated by the
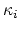 's. Since we know a priori that all the
's. Since we know a priori that all the
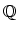 -stable classes on
-stable classes on
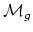 extend to
extend to
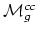 , a yes answer would lead to a new proof
of the Mumford conjecture.
Perhaps that conversely the techniques of the Madsen-Weiss proof can help
to settle this question.
, a yes answer would lead to a new proof
of the Mumford conjecture.
Perhaps that conversely the techniques of the Madsen-Weiss proof can help
to settle this question.
(b) The variety
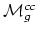 may of interest in its own right. For an
algebraic geometer it is natural to ask whether it solves a moduli
problem.
may of interest in its own right. For an
algebraic geometer it is natural to ask whether it solves a moduli
problem.
- (Vakil) Regarding Faber's conjecture, explain the intersection
number part (values of products of
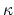 classes in
classes in
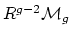 ). This is known by Virasoro methods, but this should
not be the ``real reason.'' What is the real reason? This is
related to Morita's conjecture announced at this conference
[Mor05] (Conjecture 1, p. 4). For that matter, prove Morita's
conjecture! Perhaps this is the ``right'' way to prove Faber's
intersection number conjecture.
). This is known by Virasoro methods, but this should
not be the ``real reason.'' What is the real reason? This is
related to Morita's conjecture announced at this conference
[Mor05] (Conjecture 1, p. 4). For that matter, prove Morita's
conjecture! Perhaps this is the ``right'' way to prove Faber's
intersection number conjecture.
- (Mondello) For
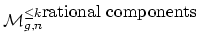 ,
is
,
is
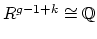 ? What is
? What is
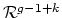 generated by? When should we expect a 1-dimensional socle, and what
should we expect for
generated by? When should we expect a 1-dimensional socle, and what
should we expect for
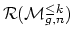 ?
?
- (Igusa) Are there operations which relate the stable classes on
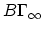 ? We have
? We have
![$ H_{spec}^*(\mathbb{CP})^\infty_{-1} \cong
\mathbb{Z}[c_1]\cdot u $](img93.png) , where
, where 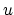 is the Thom class in degree
is the Thom class in degree 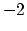 .
How is this reflected at the level of infinite loop spaces? What are
the stable maps
.
How is this reflected at the level of infinite loop spaces? What are
the stable maps
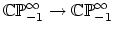 ?
?
- (Baldwin) Has anyone computed the intersection cohomology of
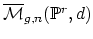 ? These can be arbitrarily singular, but
this is what intersection cohomology is designed for. Is there a good
notion of the tautological ring here? Perhaps the virtual fundamental
class plays the usual role of the fundamental class.
? These can be arbitrarily singular, but
this is what intersection cohomology is designed for. Is there a good
notion of the tautological ring here? Perhaps the virtual fundamental
class plays the usual role of the fundamental class.
- (Faber) From Ekedahl and van der Geer,
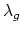 is 0 on
is 0 on
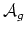 rationally but not integrally.
The order in integral cohomology has been computed up to a factor of
two. What is it? (Compare to 5 above.)
rationally but not integrally.
The order in integral cohomology has been computed up to a factor of
two. What is it? (Compare to 5 above.)
- (Bertram) When will Getzler's paper on
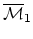 appear (even just
as a preprint)? Conjecture:
appear (even just
as a preprint)? Conjecture:
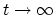 . Getzler comments that he
does not like how this question is phrased.
. Getzler comments that he
does not like how this question is phrased.
- (Ellenberg) Consider Hurwitz space (genus
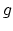 , degree
, degree 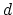 ).
Could the cohomology stabilize as
).
Could the cohomology stabilize as
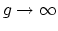 with
with 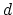 fixed? The
reason behind this question is that point counting over finite fields
gives exactly the behavior we would expect if we had Harer stability
in degree 2.
fixed? The
reason behind this question is that point counting over finite fields
gives exactly the behavior we would expect if we had Harer stability
in degree 2.
So, could some sort of Harer stability hold for some sort of Hurwitz
schemes? Motivation for this question comes from work on number
fields/function fields done in the '80s by Darskovksy and Wright.
The general philosophy is this: suppose we have a nice sequence of
varieties
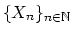 ,and
,and
exists for all 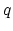 . Is this because of some version of Harer
stability at play here?
. Is this because of some version of Harer
stability at play here?
- (Tseng) Same question for
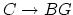 , with
, with 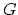 a finite group.
Tillmann says ``yes'' for
a finite group.
Tillmann says ``yes'' for 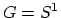 . More precisely, consider
for
. More precisely, consider
for 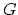 connected, such as
connected, such as 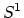 . This stabilizes by gluing in tori
and the induced map on homology is an isomorphism in some range. Is this
related?
. This stabilizes by gluing in tori
and the induced map on homology is an isomorphism in some range. Is this
related?
- (Sullivan) Fix a curve
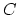 and look at all unbranched covers of
it. This gives points in
and look at all unbranched covers of
it. This gives points in
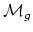 . Do these become uniformly
dense for any C (with respect to the Teichmuller metric) in
universally defined regions
. Do these become uniformly
dense for any C (with respect to the Teichmuller metric) in
universally defined regions 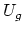 of
of
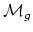 for
for 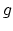 large? More precisely, given
large? More precisely, given
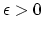 , can we find
, can we find 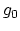 such that, for
such that, for 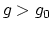 every point of
every point of 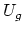 is within distance
is within distance 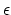 of an unbranched cover of
of an unbranched cover of
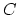 of genus
of genus 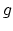 ?
This would
imply that, given curves
?
This would
imply that, given curves 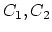 , one could find covers
, one could find covers
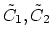 which are arbitrarily close in the moduli
space, the Siegel-Ehrenpreis problem.
which are arbitrarily close in the moduli
space, the Siegel-Ehrenpreis problem.
- (Morita) There are many numerical invariants that can be
associated to the moduli space.
- One may compute the signature of the cohomology ring of
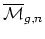 .
.
- Since
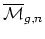 is a rational cohomology manifold, there are
Thom's rational Pontrjagin classes, and one may compute the rational
is a rational cohomology manifold, there are
Thom's rational Pontrjagin classes, and one may compute the rational
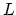 -genus with respect to these.
-genus with respect to these.
- Lastly,
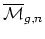 is an orbifold of a complex manifold, so
there are orbifold Chern classes, and hence orbifold Pontrjagin
classes. Thus one may talk about the orbifold
is an orbifold of a complex manifold, so
there are orbifold Chern classes, and hence orbifold Pontrjagin
classes. Thus one may talk about the orbifold 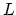 -genus.
-genus.
What are these numbers? Do they agree? Probably not, but their
disagreement would tell us interesting information about the types of
singularities in the moduli space. The difference between the
signature and the rational 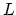 -genus detects geometric singularities.
The difference between the rational
-genus detects geometric singularities.
The difference between the rational 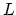 -genus and the orbifold
-genus and the orbifold
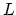 -genus detects complex analytic singularities.
-genus detects complex analytic singularities.
One may similarly ask questions about the signature of the
tautological ring, and many other variations on this theme.
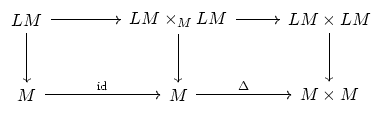
- (Sullivan) This question regards the algebraic structure on the
homology of the free loop space of a manifold. There are maps
and
First the naive question: what is the algebraic structure here? The
spectral sequence converging to
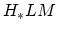 has
has 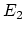 term a tensor
product of a Hopf algebra (coming from the base
term a tensor
product of a Hopf algebra (coming from the base 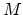 ) and a Frobenius
algebra (coming from the fibre). But the differential does not
respect these structures.
) and a Frobenius
algebra (coming from the fibre). But the differential does not
respect these structures.
A perhaps better question is: can we illuminate the situation be
reformulating in terms of the category of spaces over 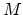 ? We have
? We have
The left square corresponds to the Frobenius algebra part, and the
right square corresponds to the Hopf algebra part. So, what is the
full algebraic structure here?
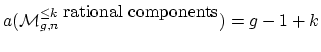 .
.
![]() has the homotopy type of a
complex of (real) dimension
has the homotopy type of a
complex of (real) dimension
![]() ? If not, is the cohomological dimension
? If not, is the cohomological dimension
![]() ? What about
quasicoherent cohomological dimension
? What about
quasicoherent cohomological dimension
![]() ? Or with
cohomology of
? Or with
cohomology of ![]() -adic sheaves, is the cohomological dimension
-adic sheaves, is the cohomological dimension
![]() ? (Note that some of these
have already been answered by Looijenga.)
? (Note that some of these
have already been answered by Looijenga.)
![]() has the homotopy type of a
finite cell complex of dimension
has the homotopy type of a
finite cell complex of dimension ![]() when
when
![]() and
and ![]() when
when
![]() (this answers part of the first question).
I would state my conjecture (in characteristic zero) not just for
(this answers part of the first question).
I would state my conjecture (in characteristic zero) not just for ![]() -adic
sheaves, but for all constructible sheaves.
-adic
sheaves, but for all constructible sheaves.
![]() gives a
Morse function on
gives a
Morse function on
![]() . (Is there a reason for Sarnak to believe
this conjecture true?)
. (Is there a reason for Sarnak to believe
this conjecture true?)
![]() on
on
![]() satisfies
satisfies
![]() . Is it zero?
Faber says yes, over a field of characteristic 2. Teleman suggests
that there are lots of natural torsion classes in
. Is it zero?
Faber says yes, over a field of characteristic 2. Teleman suggests
that there are lots of natural torsion classes in ![]() -theory
(arising from the Grotherdieck-Riemann-Roch theorem); how do they
look in cohomology? (Compare to 13 below.)
-theory
(arising from the Grotherdieck-Riemann-Roch theorem); how do they
look in cohomology? (Compare to 13 below.)
![]() 's
live on
's
live on
![]() . It is true that all of the stable classes
(so including torsion) live on the orbifold
. It is true that all of the stable classes
(so including torsion) live on the orbifold
![]() ?
?
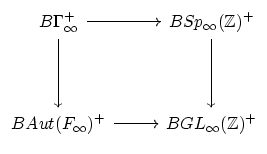
![]() to
to
![]() ? Is
? Is
![]() a
a ![]() ? Is it true that
? Is it true that
![]() is precisely the kernel of the Johnson homomorphism? Looijenga
points out that the answer to these last two questions is definitely no for large genus. By work of Johnson, the
is precisely the kernel of the Johnson homomorphism? Looijenga
points out that the answer to these last two questions is definitely no for large genus. By work of Johnson, the
![]() -cohomological dimension
of the (orbifold) fundamental group of
-cohomological dimension
of the (orbifold) fundamental group of
![]() grows like a cubic
polynomial in
grows like a cubic
polynomial in ![]() which is certainly larger than the dimension of the space
itself. Instead he proposes the following question.
which is certainly larger than the dimension of the space
itself. Instead he proposes the following question.
![]() is
is ![]() -connected with
-connected with
![]() as
as
![]() ?
?
![]() in the rational cohomology of
in the rational cohomology of ![]() is the subalgebra generated by the
is the subalgebra generated by the
![]() 's. Since we know a priori that all the
's. Since we know a priori that all the
![]() -stable classes on
-stable classes on
![]() extend to
extend to
![]() , a yes answer would lead to a new proof
of the Mumford conjecture.
Perhaps that conversely the techniques of the Madsen-Weiss proof can help
to settle this question.
, a yes answer would lead to a new proof
of the Mumford conjecture.
Perhaps that conversely the techniques of the Madsen-Weiss proof can help
to settle this question.
![]() may of interest in its own right. For an
algebraic geometer it is natural to ask whether it solves a moduli
problem.
may of interest in its own right. For an
algebraic geometer it is natural to ask whether it solves a moduli
problem.
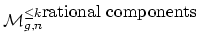 ,
is
,
is
![]() ,and
,and
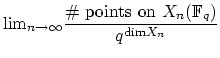
![]() ? We have
? We have