We introduce a different ![]() -adic setup for counting points (or equivalently computing zeta functions). If
-adic setup for counting points (or equivalently computing zeta functions). If ![]() is a variety over
is a variety over
![]() , we want to count points using `de Rham' cohomology. We will demonstrate Monsky-Washnitzer cohomology (a kind of rigid cohomology for smooth affine varieties). We restrict to the case where
, we want to count points using `de Rham' cohomology. We will demonstrate Monsky-Washnitzer cohomology (a kind of rigid cohomology for smooth affine varieties). We restrict to the case where ![]() is an affine curve, since in higher dimensions other methods will be faster. Then
is an affine curve, since in higher dimensions other methods will be faster. Then
![]() .
.
Let
![]() be the Witt vectors, and let
be the Witt vectors, and let ![]() be the fraction field of
be the fraction field of ![]() . Define
. Define
Let
![]() be the
be the ![]() -module generated by symbols
-module generated by symbols
![]() modulo the submodule generated by
modulo the submodule generated by
![]() . Then there is a
. Then there is a ![]() -linear derivation
-linear derivation
![]() . Letting
. Letting
![]() ; you get the de Rham complex
; you get the de Rham complex
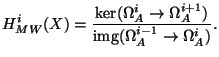
The spaces ![]() are finite-dimensional, but it is not obvious; it relies upon relating this cohomology to rigid cohomology for proper varieties, namely, crystalline cohomology which we know is finite-dimensional for other reasons. Moreover, they satisfy the Lefschetz trace formula: if
are finite-dimensional, but it is not obvious; it relies upon relating this cohomology to rigid cohomology for proper varieties, namely, crystalline cohomology which we know is finite-dimensional for other reasons. Moreover, they satisfy the Lefschetz trace formula: if ![]() is the
is the ![]() -power Frobenius, then (Monsky)
-power Frobenius, then (Monsky)
The idea: try to compute ![]() and the map induced by
and the map induced by ![]() (find
(find
![]() lifting
lifting ![]() -power Frobenius).
-power Frobenius).
Example.
Look at
![]() with
with
![]() odd. Let
odd. Let
![]() ,
, ![]() monic. Lift it to
monic. Lift it to
![]() , where
, where ![]() is monic, degree
is monic, degree ![]() over
over ![]() . It is easy to compute that
. It is easy to compute that ![]() is one-dimensional. Now
is one-dimensional. Now ![]() is generated by
is generated by ![]() for
for
![]() , and
, and
![]() ,
,
![]() . Note
. Note ![]() splits under
splits under
![]() into plus and minus eigenspaces.
into plus and minus eigenspaces.
You need to find relations in ![]() that
that
![]() . (This is a special situation: all relations are `algebraic'.) Lift the
. (This is a special situation: all relations are `algebraic'.) Lift the ![]() -power Frobenius by
-power Frobenius by ![]() by the Witt vector Frobenius,
by the Witt vector Frobenius,
![]() , and
, and
![]() . Compose this map with itself
. Compose this map with itself ![]() times to get a
times to get a ![]() -power Frobenius lift, and this allows us to compute the zeta function of a genus
-power Frobenius lift, and this allows us to compute the zeta function of a genus ![]() hyperelliptic curve over
hyperelliptic curve over
![]() in time
in time
![]() .
.
Back to the
main index
for Future directions in algorithmic number theory.