We present an algorithm which allows us to count solutions to a homogeneous equation
![]() of degree
of degree ![]() (for simplicity we assume
(for simplicity we assume ![]() ,
, ![]() ) with running time which does not increase exponentially in number of variables. In other words, we are interested in computing the number of projective solutions
) with running time which does not increase exponentially in number of variables. In other words, we are interested in computing the number of projective solutions
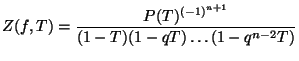
If we compute ![]() naively for
naively for
![]() then we can of course recover the polynomial
then we can of course recover the polynomial ![]() ; the time required to do this, however, requires
; the time required to do this, however, requires
![]() evaluations of
evaluations of ![]() . The input is given by
. The input is given by
![]() terms of size
terms of size ![]() , and the output size is approximately
, and the output size is approximately
![]() . We would like the running time to be polynomial in this quantity.
. We would like the running time to be polynomial in this quantity.
If ![]() , we are counting solutions of a univariate polynomial, and this can be done in time
, we are counting solutions of a univariate polynomial, and this can be done in time
![]() . For
. For ![]() , we have an algorithm of Schoof-Pila for curves which has run time
, we have an algorithm of Schoof-Pila for curves which has run time
![]() where
where ![]() depends on
depends on ![]() exponentially. In general, there is an algorithm (due to L. and Wan) which runs in time
exponentially. In general, there is an algorithm (due to L. and Wan) which runs in time
![]() . Notice the
. Notice the ![]() in the exponent--we would like to lose this dependence.
in the exponent--we would like to lose this dependence.
The new result: If ![]() is `sufficiently generic' (we exclude a Zariski closed set which is efficiently computable),
is `sufficiently generic' (we exclude a Zariski closed set which is efficiently computable), ![]() , and
, and ![]() , then we can find
, then we can find ![]() using
using
![]() bit operations. As a corollary, we see that if
bit operations. As a corollary, we see that if
![]() is sufficiently generic, then there exists an algorithm which takes as input a prime
is sufficiently generic, then there exists an algorithm which takes as input a prime ![]() , outputs the number of solutions
, outputs the number of solutions
![]() , and has run time
, and has run time
![]() .
.
Recall that
![]() , where we write
, where we write ![]() for the projective variety defined by the equation
for the projective variety defined by the equation ![]() . The action of
. The action of
![]() can be represented by a matrix with entries in a field of characteristic zero, and we find that
can be represented by a matrix with entries in a field of characteristic zero, and we find that
Instead, we work with the ![]() -adic theory, where
-adic theory, where
![]() is a
is a ![]() -module for a ring
-module for a ring
![]() . We compute instead
. We compute instead
![]() , and compute the matrix of
, and compute the matrix of
![]() . (Specifically,
. (Specifically,
![]() where
where
![]() is the unramified extension of
is the unramified extension of
![]() of degree
of degree ![]() and
and
![]() . Also our
. Also our
![]() is actually the primitive part of the cohomology space.) Consider the family
is actually the primitive part of the cohomology space.) Consider the family
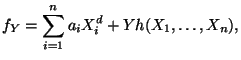
We see that
![]() where
where
![]() , and
, and ![]() is a matrix of power series around the origin satisfying the differential equation
is a matrix of power series around the origin satisfying the differential equation
![]() with initial condition
with initial condition ![]() , where
, where ![]() is easily computed. This gives a way to compute
is easily computed. This gives a way to compute
![]() in a radius around the origin, and we need to extend this to the closed disc of radius
in a radius around the origin, and we need to extend this to the closed disc of radius ![]() .
.
The entries of the matrices are ![]() -adic holomorphic functions, so to compute these modulo a power of
-adic holomorphic functions, so to compute these modulo a power of ![]() we find rational functions with denominators corresponding to the values of
we find rational functions with denominators corresponding to the values of ![]() where the variety becomes singular and then recover the numerator from the power series. Using overconvergence we get a bound on the degree of these rational functions. We evaluate the rational functions at
where the variety becomes singular and then recover the numerator from the power series. Using overconvergence we get a bound on the degree of these rational functions. We evaluate the rational functions at ![]() . One gets nice complexity because we work with univariate power series, with decay in the coefficients on the order of
. One gets nice complexity because we work with univariate power series, with decay in the coefficients on the order of ![]() , and one needs to take the power of
, and one needs to take the power of ![]() approximately on the order of
approximately on the order of
![]() .
.
In the old algorithm, we would work in
![]() , the ring of power series in
, the ring of power series in
![]() over an
over an
![]() where
where
![]() is the unramified extension of
is the unramified extension of
![]() of degree
of degree ![]() (if
(if ![]() ) and
) and
![]() modulo an infinite subspace; the power series we must work with have on the order of
modulo an infinite subspace; the power series we must work with have on the order of
![]() terms.
terms.
Problem.
Find an algorithm which counts the number of points on a curve in time
![]() .
.
Back to the
main index
for Future directions in algorithmic number theory.