Heath-Brown: Rational Points and Analytic Number Theory

Analytic number theory is often quite useful in questions on rational points on varieties. For example, using the circle method, weak approximation gives formulas of the type

$$N(B) \sim CB^k(\log B)^j$$

where

$$C=\sigma_\infty \prod_p \sigma_p.$$

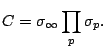
What kind of asymptotic formulae can we expect when weak approximation fails?

Look at

$$L_1(x_1,x_2)L_2(x_1,x_2) = x_3^2+x_4^2$$

$$L_3(x_1,x_2)L_4(x_1,x_2) = x_5^2+x_6^2$$

where $L_i(x_1,x_2)$ are linear forms over $\mathbb{Z}$. This is the intersection of two quadrics in $\mathbb{P}^5$. In this case, the Hasse principle may fail, and weak approximation may fail. We take

$$H(x_1,\dots,x_6)=\max(\vert x_1\vert,\vert x_2\vert).$$

We have the following ``theorem'': There is a modification of the Hardy-Littlewood formula in which

$$C=\kappa \sigma_\infty \prod_p \sigma_p$$

where $\kappa \in [0,2]$, $\kappa$ vanishes precisely when the Hasse principle fails, $\kappa$ is built from information at a finite number of `bad' places, and $\kappa \in \mathbb{Q}$ is easily calculable. To do this, use a ``descent'' process followed by variation of the circle method.

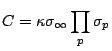
Theorem. [H-B, Moroz] Let $a,b \in \mathbb{N}$ be coprime, with $a \equiv \pm 2,\pm 3 \pmod{9}$. Then the surface

$$x_1^3+2x_2^3+ax_3^3+bx_4^3=0$$

has a nontrivial rational point.

To prove this, there are two ingredients. First, a result of Satgé: $x_1^3+2x_2^3=p$ has a rational point if $p$ is prime, $p \equiv 2 \pmod{9}$ (proved by Heegner point construction). Second, $ax_3^3+bx_4^3$ takes infinitely many prime values $2 \pmod{9}$.

In the other direction, analytic number theorists are often interested in rational points on varieties. We take the counting function

$$N(F;B)=\char93 \{F(x_1,\dots,x_n)=0:\max\vert x_i\vert \leq B,\ x \in \mathbb{Z}^n\}.$$

For instance, take $F(x)=a_1 x_1^3 + \dots + a_n x_n^3$; there exists an asymptotic formula $n \geq 8$ (Vaughan). In the case $n=7$, analytic methods establish a local-global principle, but not an asymptotic formula. To handle this case, we would want:

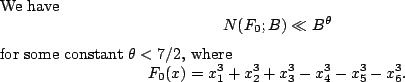
This is known for any $\theta > 7/2$, and conjectured to be true for any $\theta>3$, so it is reasonable to expect.

What about $N(F_0,B)$ for $F_0=x_1^d+x_2^d+x_3^d-x_4^d-x_5^d-x_6^d$? We can show $\theta < 7/2$ for $d \geq 24$. This variety has lines in trivial planes of the type $x_1=x_4,x_2=x_5,x_3=x_6$, and no other lines if $d \geq 5$; what other quadric or low degree curves can be found?

Proposition. [Green 1975] Any curve of genus 0 or $1$ in $F_0=0$ has $x_i/x_j$ constant for some $i,j$, as soon as $d \geq 25$.

(Here $25=(6-1)^2$.) This involves meromorphic functions and Nevanlinna theory.

Proposition. [Davenport 1963] Any cubic form $F(x) \in \mathbb{Z}[x]$ in $n \geq 16$ variables has a nontrivial integer zero.

This applies to an arbitrary cubic form; there is a better result for smooth forms with $n \geq 9$. Define a matrix $J(X)$ with entries

$$J(X)_{ij}=\frac{\partial^2 F}{\partial x_i \partial x_j}$$

and $V_m=\{x:{\mathrm{rk}}J(x) \leq m\} \subset \mathbb{P}^{m-1}$. Assume that $F(x)=0$ has no nontrivial rational point; then any component $C$ of $V_m$ which has a rational point has $\dim C \leq m-1$.

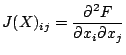
Vinogradov's mean value theorem refers to the counting function of the variety defined by the equations

$$x_1^j+\dots+x_s^j=y_1^j+\dots+y_s^j$$

for $1 \leq j \leq k$, $V(k,s) \subset \mathbb{P}^{2s-1}$, count $0 < x_i,y_i \leq B$. This is a cone with vertex $(1:\dots:1;1:\dots:1)$.

One can easily show $N(B) \gg B^s,B^{2s-k(k+1)/2}$ for all $s,k$; if $k \geq s$ then $x$ is a permutation of $y$, $N(B) \sim s! B^s$. In fact, $N(B) \sim cB^s$ for $s=k+1$ (Vaughan, Wooley).

For $s \geq s_0(k) \sim k^2\log k$, we have $N(B) \sim cB^{2s-k(k+1)/2}$.

Applications: Exponential sums, zero-free region for $\zeta(s)$ and the error term in the prime number theorem. So this question has several far-reaching implications!

Back to the main index for Rational and integral points on higher dimensional varieties.