Rotger: Shimura varieties

Let $ \overline{k}$ be an algebraically closed field, $ A$, $ \mathcal{L}/\overline{k}$ a polarized abelian variety. We are interested in:

  1. Field of moduli of $ (A, \mathcal{L})$ and field of moduli of $ {\mathrm{End}}(A)$
  2. Fields of definition of $ (A, \mathcal{L})$ and fields of definition of $ {\mathrm{End}}(A)$.

The field of moduli of $ (A, \mathcal{L})$ $ \mathcal{K}_{A, \mathcal{L}}$ is the unique minimal field in $ \overline{k}$ such that $ (A, \mathcal{L})^\sigma \iso (A, \mathcal{L})$ for all $ \sigma \in {\mathrm{Gal}}(\overline{k}/\mathcal{K}_{A, \mathcal{L}}$).

$\displaystyle \xymatrix{&&\mathcal{K}_{\mathrm{End}(A)}\\ & \mathcal{K}_S \ar@{-}[ur]& \\ \mathcal{K}_{(A, \mathcal{L})}\ar@{-}[ur] &&}$    

$ \mathbb{Z} \subset S \subset {\mathrm{End}}(A)$. The top field is the unique field fixed by all $ \sigma$ such that there exists $ A \iso A^\sigma$ making the following diagram commute:

$\displaystyle \xymatrix{A \ar[r]\ar[d]_{\beta \in {\mathrm{End}}(A)} & A^\sigma \ar[d]^{\beta^\sigma}\\ A \ar [r] & A^\sigma }$    

Shimura: the generic odd dimensional polarized abelian variety admits a model over $ \mathcal{K}_{A, \mathcal{L}}$. The generic even dimensional polarized abelian variety does not admit a model over $ \mathcal{K}_{A, \mathcal{L}}$.

(Silverberg) Fix $ \mathcal{K}_{A, \mathcal{L}}$. There is a (unique, Galois) minimal field of definition $ \mathcal{K}_S/K_{(A, \mathcal{L})}$ of $ S \subset {\mathrm{End}}(A)$.

(Silverberg) There is a $ H_{d,r}$ such that $ \vert{\mathrm{Gal}}(K_S/K_{A, \mathcal{L}})\vert \leq H_{d,r}$ for any abelian variety $ A$ such that $ \dim A = d$ and $ S \subset {\mathrm{End}}(A)$ with $ [S:\mathbb{Z}] = r$.

If $ A$ is simple, $ {\mathrm{End}}(A)$ is an order in either a totally real field, a division algebra over a CM-field, or a quaternion algebra.

We will focus on the latter case.


Forgetful maps between Shimura varieties and rational points

Let $ F$ be a totally real number field, with $ [F:\mathbb{Q}] = n$. Let $ B$ be an indefinite quaternion algebra over $ F$ (that is, $ B \tensor_{\mathbb{Q}} \mathbb{R} \iso M_2(\mathbb{R})^n$). Let $ \mathcal{O}_B$ be a maximal order in $ B$. Let

$\displaystyle \Gamma_B = \{ \gamma \in \mathcal{O}_B: N_{B/F}(\gamma) = 1\} \subset SL_2(\mathbb{R})^n.$    

Moduli problem $ (\mathcal{O}_B, \mu)$: classify principally polarized abelian varieties $ (A, i, \mathcal{L})$ where $ A$ is an abelian variety of $ \dim A = 2n$, $ i: \mathcal{O}_B \into {\mathrm{End}}(A)$,and the Rosati involution has the form $ *_{\mathcal{L}}: \mathcal{O}_B \rightarrow \mathcal{O}_B$, $ b \mapsto \mu^{-1}\overline{b}\mu$ where $ \mu \in \mathcal{O}_B$ such that $ \mu^2 + \delta = 0$ and $ \delta \in F^\times$.


\begin{proposition} If $(A, \mathcal{L})$\ is a principally polarized abelian v... ...\ is a totally positive generator of $\operatorname{disc}(B)$. \end{proposition}

(Shimura): The moduli functor is coarsely represented over $ \mathbb{Q}$ by a complete algebraic variety $ X_D/\mathbb{Q} = X_{(\mathcal{O}_B, \mu)}/\mathbb{Q}$, with $ \dim X_D = n$. We havea $ X_D(\mathbb{C}) = \Gamma_B\backslash \mathfrak{h}^n$, where $ \mathfrak{h}$ is the Poincaré upper half plane.

Let $ R_F$ be the ring of integers of $ F$, $ R_F \subset S \subset \mathcal{O}_B$, where $ S$ is a totally real quadratic order over $ R_F$. There are forgetful finite maps over $ \mathbb{Q}$

$\displaystyle \xymatrix{ X_{\mathcal{O}_B, \mu} \ar[r] & \mathcal{M}_S \ar[r] &... ...ert->}[r]& [A, i\vert _{R_F} , \mathcal{L}] \ar@{\vert->}[r]& [A, \mathcal{L}]}$    

where $ \mathcal{M}$ is the Hilbert modular variety classifying varieties with real multiplication by the subscript. The dimensions of these moduli spaces are, respectively, $ n$, $ n$, $ 3n$, $ 2n^2 + n$.

     

The picture in $ n =1 $ is

Shimura curve: $ X_{(\mathcal{O}, \mu)}$$\displaystyle \rightarrow$   Hilbert surface: $ \mathcal{M}_S$$\displaystyle \rightarrow$   Igusa's space: $ \mathcal{A}_2$$\displaystyle .$    

We have a tower of fields

$\displaystyle \mathcal{K}_{{\mathrm{End}}(A)} = \mathbb{Q}(P) \subset \mathcal{... ...= \mathbb{Q}(P\vert _F) \subset \mathcal{K}_{A, \mathcal{L}} = \mathbb{Q}(P_0).$    

The automorphism group of $ X_D = X_{(\mathcal{O}_{B},\mu)}$: is

$\displaystyle (\mathbb{Z}/2)^{2r} \iso W = \frac{\mathrm{Norm}_{B_+^\times}(\Gamma_B)}{\Gamma_B \cdot F^\times}\subset {\mathrm{Aut}}_{\mathbb{Q}(X_D)}$    

where $ 2r = \char93 \{ \mathfrak{p}\vert\operatorname{disc}(B)\}$.


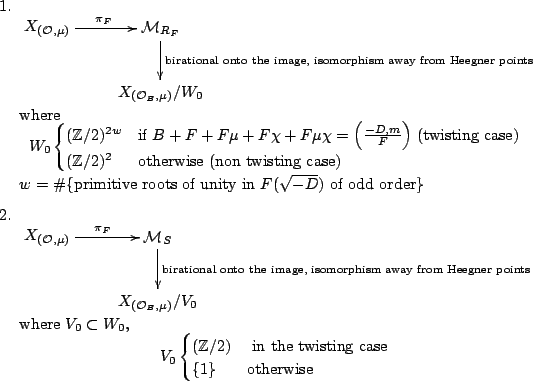
\begin{theorem} \begin{enumerate} \item \begin{equation*} \xymatrix{ X_{(\ma... ...{1\} & \text{otherwise} \end{cases}\end{equation*} \end{enumerate}\end{theorem}


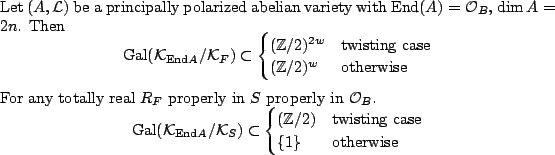
\begin{corollary} Let $(A, \mathcal{L})$\ be a principally polarized abelian va... ...ng case}\\ \{1\} & \text{otherwise} \end{cases} \end{equation*}\end{corollary}


Field of definition for abelian surfaces

Let $ (A, \mathcal{L})/K$ be a principally polarized abelian surface over a number field $ K$ with $ {\mathrm{End}}_{\overline{K}}(A) = \mathcal{O}_B$, $ \operatorname{disc}(B) = D$. There is a diagram

$\displaystyle \xymatrix{ & K_{{\mathrm{End}}(A)}\ar@{-}[dr]^{\text{$\vert G\ver... ...re)}} & & \mathcal{K}_{{\mathrm{End}}(A)} \\ & \mathcal{K}_{A, \mathcal{L}} & }$    

  1. If $ B = \left(\frac{-D, m}{\mathbb{Q}}\right)$ for $ 0 < m < D$, $ m\vert D$, then (with Dieulefait)

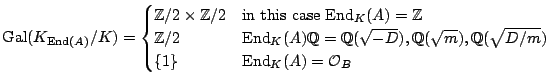    $\displaystyle {\mathrm{Gal}}(K_{{\mathrm{End}}(A)}/K) = \begin{cases}\mathbb{Z}... ...sqrt{D/m})$}\\ \{1\} & \text{${\mathrm{End}}_K(A) = \mathcal{O}_B$} \end{cases}$    

  2. Otherwise,

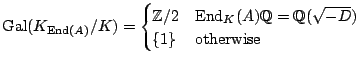    $\displaystyle {\mathrm{Gal}}(K_{{\mathrm{End}}(A)}/K) = \begin{cases}\mathbb{Z}... ...tensor \mathbb{Q}= \mathbb{Q}(\sqrt{-D})\\ \{1\} & \text{otherwise} \end{cases}$    



Back to the main index for Rational and integral points on higher dimensional varieties.