Introduction
The circle method is the Hardy-Littlewood method (1920s), ``any method involving Harmonic analysis that counts solutions of Diophantine questions'', including Kloosterman methods.
Example.
Consider a homogeneous polynomial
![]() of degree
of degree ![]() . We count
. We count
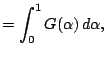 |
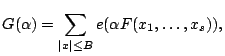
Let
![]() as
as
![]() as slowly as you like,
as slowly as you like,
![]() . We look at
. We look at
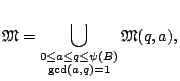
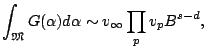
For
![]() , the minor arcs, then
, the minor arcs, then ![]() should be ``randomly'' behaved, so one tries to show:
should be ``randomly'' behaved, so one tries to show:
![]() when
when
![]() . If true, then
. If true, then
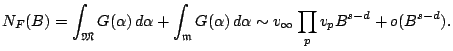
In particular, this will not work for varieties which fail the Hasse principle. The basic techniques work for all number fields
![]() , or even for
, or even for
![]() or other function fields.
or other function fields.
Scope of the Circle Method
The circle method works with ``sufficiently many'' variables.
Proposition. [Birch 1957]
Given forms
![]() , of respectively odd degrees
, of respectively odd degrees
![]() , and provided that
, and provided that
![]() is large enough, then there exists a rational point on
is large enough, then there exists a rational point on
![]() .
.
This method diagonalizes each of the forms, but at a great cost:
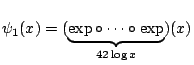 ,
,
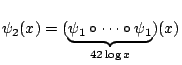 and so on.
and so on.
Example.
For ![]() , one has
, one has ![]() (Davenport 1963);
(Davenport 1963);
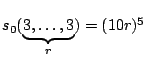 (Schmidt 1984).
(Schmidt 1984).
![]() (Dietmann-W).
(Dietmann-W).
Proposition. [Birch 1962]
Let
![]() be homogeneous of degree
be homogeneous of degree ![]() . Let
. Let
![]() . Then whenever
. Then whenever
![]() , one has
, one has ![]() asymptotic to a product of local densities as before.
asymptotic to a product of local densities as before.
The difficulty of this result depends on the singular locus being reasonably small in dimension. This holds for any number field, and it is probable that this holds for a function field assuming the characteristic is sufficiently large.
Proposition. [Heath-Brown 1983, Hooley 1988]
For ![]() , we have the Hasse principle for nonsingular cubic forms.
, we have the Hasse principle for nonsingular cubic forms.
We now turn to some simpler situations.
Proposition. [Brudem-W]
If
![]() ,
,
![]() binary, homogeneous of degree
binary, homogeneous of degree ![]() , then
, then ![]() is asymptotic to the product of local densities whenever
is asymptotic to the product of local densities whenever
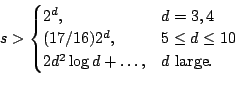
For a diagonal form
![]() , work by Hua, Vaughan, Heath-Brown, the same conclusion holds for
, work by Hua, Vaughan, Heath-Brown, the same conclusion holds for
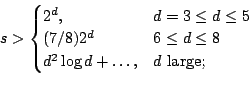
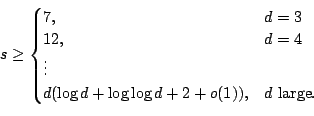
Presumably: ![]() should suffice for the method to work.
should suffice for the method to work.
Simultaneous equations: we expect need ![]() variables for
variables for ![]() form of degree
form of degree ![]() makes it look we need
makes it look we need ![]() variables for
variables for ![]() forms of degree
forms of degree ![]() . For
. For
![]() , (
, (
![]() ), the number of variables required is given by: if the forms are in general position, and
), the number of variables required is given by: if the forms are in general position, and
![]() , then we have an asymptotic formula. For
, then we have an asymptotic formula. For ![]() diagonal cubics,
diagonal cubics,
![]() . For
. For ![]() diagonal cubics, one has the Hasse principle whenever
diagonal cubics, one has the Hasse principle whenever ![]() (Brudeur, W).
(Brudeur, W).
Keys to Success
We have the major arcs
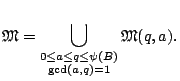
For
![]() a rational number, we have
a rational number, we have
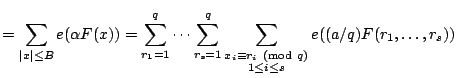 |
||
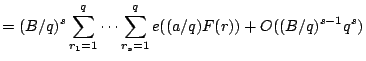 |
||
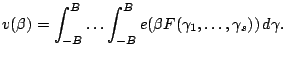
For the minor arcs, we want to show
![]() . One has Weyl differencing: letting
. One has Weyl differencing: letting
![]() , we have
, we have
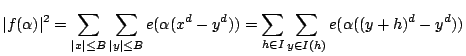
Finally, there is recent work of Heath-Brown and Skorobogatov: For
![]() ,
, ![]() a norm form of degree
a norm form of degree ![]() , then the Brauer-Manin obstruction is the only one to weak approximation and the Hasse principle. One uses descent to
, then the Brauer-Manin obstruction is the only one to weak approximation and the Hasse principle. One uses descent to
![]() , where the circle method gives weak approximation and the Hasse principle. One can generalize this to the case
, where the circle method gives weak approximation and the Hasse principle. One can generalize this to the case
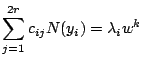
Back to the
main index
for Rational and integral points on higher dimensional varieties.