The C*-algebra of Bost--Connes
We give a different construction of the 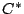 -algebra of
Bost-Connes to that found in their original paper. It is directly
inspired by work of Arledge-Laca-Raeburn. Let
-algebra of
Bost-Connes to that found in their original paper. It is directly
inspired by work of Arledge-Laca-Raeburn. Let 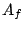 denote the
ring of finite adeles of
denote the
ring of finite adeles of 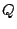 , that is the restricted
product of
, that is the restricted
product of 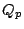 with respect to
with respect to 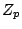 as
as 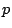 ranges over the finite primes. Recall that this restricted product
consists of the infinite vectors
ranges over the finite primes. Recall that this restricted product
consists of the infinite vectors 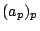 , indexed by the primes
, indexed by the primes
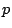 , such that
, such that
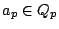 with
with
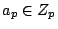 for almost all primes
for almost all primes 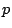 . The group of (finite) ideles
. The group of (finite) ideles 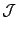 consists of the invertible elements of the adeles. Let
consists of the invertible elements of the adeles. Let
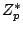 be those elements of
be those elements of
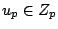 with
with
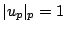 . Notice that an idele
. Notice that an idele 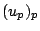 has
has
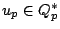 with
with
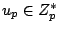 for almost all primes
for almost all primes 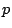 .
Let
.
Let
Further, let 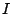 denoted the semigroup of integral ideals of
denoted the semigroup of integral ideals of
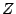 , which are of the form
, which are of the form 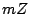 where
where
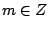 . Notice that
. Notice that 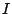 as above is also a semigroup.
We have a natural short exact sequence,
as above is also a semigroup.
We have a natural short exact sequence,
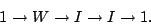 |
(1) |
The map
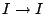 in this short exact sequence is
given as follows. To
in this short exact sequence is
given as follows. To 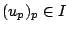 associate the ideal
associate the ideal
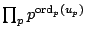 where
where
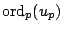 is
determined by the formula
is
determined by the formula
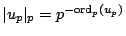 . By the
Strong Approximation Theorem we have
. By the
Strong Approximation Theorem we have
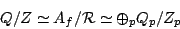 |
(2) |
and we have therefore a natural action of 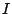 on
on
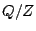 by multiplication in
by multiplication in
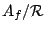 and transport
of structure. We have the following straightforward Lemmata
and transport
of structure. We have the following straightforward Lemmata
Lemma 1. For
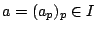 and
and
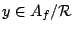 , the
equation
, the
equation
has
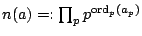 solutions in
solutions in
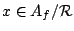 . Denote these solutions by
. Denote these solutions by ![$[x:ax=y]$](img37.gif) .
.
Let
![${\mathbb C}[A_f/{\mathcal R}]=:{\rm span}\{\delta_x:x\in
A_f/{\mathcal R}\}$](img38.gif) be the group algebra of
be the group algebra of
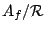 over
over
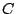 , so that
, so that
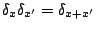 for
for
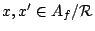 . We have,
. We have,
Lemma 2. The formula
for 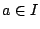 defines an action of
defines an action of 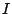 by endomorphisms of
by endomorphisms of
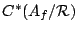 .
.
We now appeal to the notion of semigroup crossed product developed
by Laca and Raeburn, applying it to our situation. A covariant
representation of
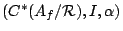 is a pair
is a pair
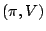 where
where
is a unital representation and
is an isometric representation in the bounded operators in a
Hilbert space 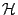 . The pair
. The pair 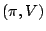 is required to satisfy,
is required to satisfy,
Such a representation is given by 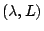 on
on
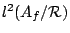 with orthonormal basis
with orthonormal basis
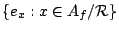 where
where
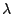 is the left regular representation of
is the left regular representation of
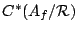 on
on
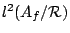 and
and
The universal covariant representation, through which all other
covariant representations factor, is called the (semigroup)
crossed product
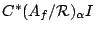 . This algebra
is the universal
. This algebra
is the universal 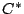 -algebra generated by the symbols
-algebra generated by the symbols
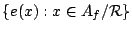 and
and
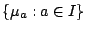 subject to the
relations
subject to the
relations
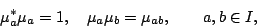 |
(3) |
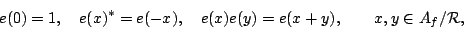 |
(4) |
![\begin{displaymath}
\frac1{n(a)}\sum_{[x:ax=y]}e(x)=\mu_ae(y)\mu_a^*,\qquad a\in
I,y\in A_f/{\mathcal R}.
\end{displaymath}](img61.gif) |
(5) |
When 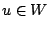 then
then 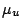 is unitary, so that
is unitary, so that
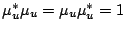 and we have for all
and we have for all
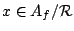 ,
,
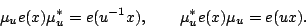 |
(6) |
Therefore we have a natural action of 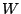 as inner automorphisms
of
as inner automorphisms
of
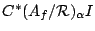 .
.
To recover the 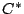 -algebra of Bost-Connes we must split the
above short exact sequence. Let
-algebra of Bost-Connes we must split the
above short exact sequence. Let 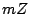 ,
,
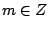 ,
be an ideal in
,
be an ideal in 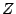 . This generator
. This generator 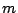 is determined up
to sign. Consider the image of
is determined up
to sign. Consider the image of 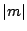 in
in 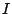 under the diagonal
embedding
under the diagonal
embedding 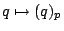 of
of 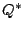 into
into 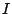 , where the
, where the
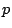 -th component of
-th component of 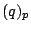 is the image of
is the image of 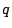 in
in
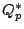 under the natural embedding of
under the natural embedding of 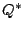 into
into
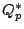 . The map
. The map
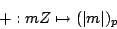 |
(7) |
defines a splitting of the short exact sequence. Let 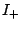 denote
the image and define
denote
the image and define 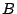 to be the semigroup crossed product
to be the semigroup crossed product
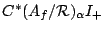 with the restricted action
with the restricted action
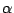 from
from 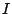 to
to 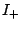 . By transport of structure, this
algebra is easily seen to be isomorphic to a semigroup crossed
product of
. By transport of structure, this
algebra is easily seen to be isomorphic to a semigroup crossed
product of
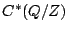 by
by 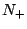 ,
where
,
where 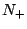 denotes the positive natural numbers. This
is the algebra of Bost-Connes. The replacement of
denotes the positive natural numbers. This
is the algebra of Bost-Connes. The replacement of 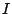 by
by 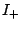 now means that the group
now means that the group 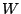 acts by outer automorphisms. For
acts by outer automorphisms. For
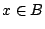 , one has that
, one has that 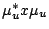 is still in
is still in 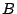 (computing
in the larger algebra
(computing
in the larger algebra
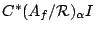 ), but
now this defines an outer action of
), but
now this defines an outer action of 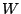 . This coincides with the
definition of
. This coincides with the
definition of 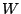 as the symmetry group as in the paper of
Bost-Connes.
as the symmetry group as in the paper of
Bost-Connes.
Back to the
main index
for The Riemann Hypothesis.
![]() -algebra of
Bost-Connes to that found in their original paper. It is directly
inspired by work of Arledge-Laca-Raeburn. Let
-algebra of
Bost-Connes to that found in their original paper. It is directly
inspired by work of Arledge-Laca-Raeburn. Let ![]() denote the
ring of finite adeles of
denote the
ring of finite adeles of ![]() , that is the restricted
product of
, that is the restricted
product of ![]() with respect to
with respect to ![]() as
as ![]() ranges over the finite primes. Recall that this restricted product
consists of the infinite vectors
ranges over the finite primes. Recall that this restricted product
consists of the infinite vectors ![]() , indexed by the primes
, indexed by the primes
![]() , such that
, such that
![]() with
with
![]() for almost all primes
for almost all primes ![]() . The group of (finite) ideles
. The group of (finite) ideles ![]() consists of the invertible elements of the adeles. Let
consists of the invertible elements of the adeles. Let
![]() be those elements of
be those elements of
![]() with
with
![]() . Notice that an idele
. Notice that an idele ![]() has
has
![]() with
with
![]() for almost all primes
for almost all primes ![]() .
Let
.
Let
![]() and
and
![]() , the
equation
, the
equation
![]() be the group algebra of
be the group algebra of
![]() over
over
![]() , so that
, so that
![]() for
for
![]() . We have,
. We have,
![\begin{displaymath}
\alpha_a(\delta_y)=\frac1{n(a)}\sum_{[x:ax=y]}\delta_x
\end{displaymath}](img42.gif)
![]() is a pair
is a pair
![]() where
where
![\begin{displaymath}
L_ae_y=\frac1{\sqrt {n(a)}}\sum_{[x:ax=y]}e_x.
\end{displaymath}](img55.gif)
![\begin{displaymath}
\frac1{n(a)}\sum_{[x:ax=y]}e(x)=\mu_ae(y)\mu_a^*,\qquad a\in
I,y\in A_f/{\mathcal R}.
\end{displaymath}](img61.gif)
![]() -algebra of Bost-Connes we must split the
above short exact sequence. Let
-algebra of Bost-Connes we must split the
above short exact sequence. Let ![]() ,
,
![]() ,
be an ideal in
,
be an ideal in ![]() . This generator
. This generator ![]() is determined up
to sign. Consider the image of
is determined up
to sign. Consider the image of ![]() in
in ![]() under the diagonal
embedding
under the diagonal
embedding ![]() of
of ![]() into
into ![]() , where the
, where the
![]() -th component of
-th component of ![]() is the image of
is the image of ![]() in
in
![]() under the natural embedding of
under the natural embedding of ![]() into
into
![]() . The map
. The map