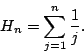The sum of divisors of $n$
Let
denote the sum of the divisors of 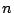 .
.
G. Robin [
MR 86f:11069] showed that the Riemann Hypothesis is
equivalent to
for all 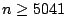 , where
, where 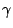 is Euler's constant.
That inequality does not leave much to spare, for Gronwall showed
is Euler's constant.
That inequality does not leave much to spare, for Gronwall showed
and Robin showed unconditionally that
for 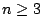 .
.
J. Lagarias [
arXiv:math.NT/0008177] elaborated on Robin's
work and showed that the Riemann Hypothesis is equivalent to
for all 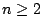 , where
, where 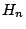 is the harmonic number
is the harmonic number
By definition,
so Lagarias' and Robin's inequalities are the same to leading order.
Back to the
main index
for The Riemann Hypothesis.