Dynamical zeta-functions

For several decades now there has been interest amongst physicists and mathematicians to study the statistics of the eigenvalue spectra of physical systems - especially those with a classical counterpart which displays chaotic behaviour. One particular goal is to try to detect in the statistical distribution of a set of energy eigenvalues an indication of whether the corresponding classical system behaves chaoticly or integrably. The answer was suggested by Berry and Tabor in 1977, and examined in depth by Bohigas, Giannoni and Schmit [ MR 85f:58034], and reveals that while classically integrable (non-chaotic) systems have a spectrum of uncorrelated eigenvalues, the spectra of classically chaotic systems show the characteristic correlations seen in the spectra of ensembles of random matrices. In particular, the semiclassical spectra of physical systems which are not symmetric under time-reversal have the same local statistics (those of the ensemble of unitary matrices, $U(N)$, with Haar measure) as the zeros high on the critical line of the Riemann zeta function and other $L$-functions.

Thus for a given physical system which possesses the correct symmetries, we can construct a zeta function which will have zeros correlated on a local scale like those of the Riemann zeta function. For a system with a Hamiltonian operator $H$ and a set of eigenvalues $E_n$, satisfying

$$H\psi_n(\bf {r})=E_n\psi_n(\bf {r}),$$

with wavefunctions $\psi_n$, a natural function to study is the spectral determinant

$$\Delta(E) \equiv \det[A(E,H)(E-H)] = \prod_j[ A(E,E_j)(E-E_j)],$$

where $A$ has no real zeros and is included so as to make the product converge.

A semiclassical expression for the spectral determinant can be given using only classical attributes of the system in question. Following Berry and Keating [ MR 92m:81053], we can write

$$\Delta(E)\sim B(E) \exp(-i\pi \overline{N}(E)) \prod_p \exp \... ...c{\exp(ikS_p/\hbar)} {k\sqrt{\vert\det(M_p^k-1)\vert}} \right).$$

Here $B(E)$ is a real function with no zeros and

$$\frac{d \overline{N}(E)}{dE}=\overline{d}(E),$$

the mean density of eigenvalues. The sum is over the periodic orbits of the classical system, $S_p$ is the action of the orbit $p$, and $M_p$ is the monodromy matrix which describes flow linearized around the orbit.

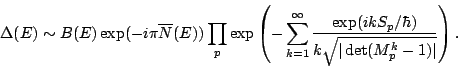
We can now define the dynamical zeta function

$$Z(E)=\prod_p \exp \left( -\sum_{k=1}^{\infty} \frac{\exp(ikS_p/\hbar)} {k\sqrt{\vert\det(M_p^k-1)\vert}} \right).$$

Since $B(E)$ has no zeros, the zeros of $Z(E)$ are the eigenvalues of the system under investigation.

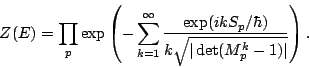
Back to the main index for The Riemann Hypothesis.