Curvature prescription
Everything below will take place in the setting of Riemannian
manifolds (or Riemannian conformal manifolds) of even dimension ![]() .
Of course many statements will also be true for odd-dimensional
manifolds and/or pseudo-Riemannian (conformal) manifolds, but our main
intent is to make this blurb readable.
There will be no reference
list here, though there are plans to compile a separate reading list
(of real papers) on the topic.
.
Of course many statements will also be true for odd-dimensional
manifolds and/or pseudo-Riemannian (conformal) manifolds, but our main
intent is to make this blurb readable.
There will be no reference
list here, though there are plans to compile a separate reading list
(of real papers) on the topic.
A touchstone in Differential Geometry is the Yamabe equation:
for ![]() ,
,
Exercise 1.
Show that (![]() ) implies the conformal change law
for the conformal Laplacian
) implies the conformal change law
for the conformal Laplacian
When ![]() , the equation governing the conformal change of
, the equation governing the conformal change of ![]() is
qualitatively different from a PDE standpoint:
is
qualitatively different from a PDE standpoint:
There is a formal procedure of analytic continuation in dimension
(which in fact can be made rigorous) that allows one to guess
(or prove) (![]() given (
given (![]() )). The Yamabe equation may be
rewritten as
)). The Yamabe equation may be
rewritten as
Exercise 2 (following C.R. Graham).
Make the dimensional continuation
argument rigorous by looking at stabilisations of the manifold ![]() ,
i.e. the
,
i.e. the ![]() -dimensional manifolds
-dimensional manifolds ![]() , where
, where ![]() is the
standard
is the
standard ![]() -torus.
-torus.
There is a generalisation of this whole picture to higher order,
in which the role of the pair ![]() is played by a pair
is played by a pair
![]() consisting of an operator and a local scalar invariant.
The
consisting of an operator and a local scalar invariant.
The ![]() are the celebrated Graham-Jenne-Mason-Sparling (GJMS)
operators, which by construction have the following properties.
are the celebrated Graham-Jenne-Mason-Sparling (GJMS)
operators, which by construction have the following properties.
With these properties, conditions are right to generalise the Yamabe
equation to
where
Exercise 3. Show that if we have a local invariant ![]() satisfying
a conformal change law like (
satisfying
a conformal change law like (![]() ,
,
![]() , with
, with
![]() a natural differential operator, then necessarily
a natural differential operator, then necessarily ![]() is conformally
invariant in the sense
is conformally
invariant in the sense
![]() .
.
The fact that ![]() has an expression with rational dependence on the
dimension is crucial to making the analytic continuation rigorous,
whether one does it by stablilisation (generalising Exercise
2), or by an algebraic argument using
has an expression with rational dependence on the
dimension is crucial to making the analytic continuation rigorous,
whether one does it by stablilisation (generalising Exercise
2), or by an algebraic argument using
![]() -linear
combinations in a dimension-stable basis of invariants.
-linear
combinations in a dimension-stable basis of invariants.
Very explicit formulas for ![]() and
and ![]() are
known up to
are
known up to ![]() . The
. The ![]() case, which was already being discussed
in the early 1980's, is particularly appealing as a source of intuition,
since the formulas there are still quite manageable. Let
case, which was already being discussed
in the early 1980's, is particularly appealing as a source of intuition,
since the formulas there are still quite manageable. Let ![]() be the
Ricci tensor and let
be the
Ricci tensor and let
The transition from ![]() to
to ![]() already points up the fact that the
already points up the fact that the
![]() are not uniquely determined: if
are not uniquely determined: if ![]() is the Weyl conformal
curvature tensor, we could add a suitable multiple of
is the Weyl conformal
curvature tensor, we could add a suitable multiple of ![]() to
to ![]() without
destroying any of its defining properties. (The coefficient should
be rational in
without
destroying any of its defining properties. (The coefficient should
be rational in ![]() , should have a zero at
, should have a zero at ![]() ,
and should not have poles that create
new ``bad'' dimensions.)
,
and should not have poles that create
new ``bad'' dimensions.)
The ![]() situation is also already big enough to show that the study
of
situation is also already big enough to show that the study
of ![]() is not just a disguised
study of the conformal properties of the Pfaffian
is not just a disguised
study of the conformal properties of the Pfaffian
![]() . One of the salient properties of the Pfaffian is that
it can be written as a polynomial in
. One of the salient properties of the Pfaffian is that
it can be written as a polynomial in ![]() , without any explicit
occurrences of
, without any explicit
occurrences of ![]() . For example, in dimension 4,
. For example, in dimension 4,
All the conformal change laws we've mentioned are good in odd dimensions,
and that for ![]() in dimension 3 shows that very strange nonlinearities
can occur:
in dimension 3 shows that very strange nonlinearities
can occur:
Back to the general case, a celebrated property of ![]() is the conformal
invariance of its integral on compact manifolds:
is the conformal
invariance of its integral on compact manifolds:
Relativistic considerations
The Einstein equations are obtained by taking the Einstein-Hilbert
action ![]() in dimension 4, and taking the total metric
variation. This means we take a compactly supported
symmetric tensor
in dimension 4, and taking the total metric
variation. This means we take a compactly supported
symmetric tensor ![]() and a curve
of metrics
and a curve
of metrics ![]() with
with
![]() , and compute that
, and compute that
Weyl relativity is one proposal for replacing the Einstein-Hilbert
action with an action that is invariant under multiplication of the
metric by a positive constant: under the variation above,
In attempting to generalise this to higher dimensions, it's clear that
![]() won't help - its total metric variation is 0, since it's a
topological invariant. Choices like
won't help - its total metric variation is 0, since it's a
topological invariant. Choices like ![]() for
for
![]() are uninteresting because the linearisations of the
analogues of the operators (
are uninteresting because the linearisations of the
analogues of the operators (![]() ) have order lower than one
might hope for - less than
) have order lower than one
might hope for - less than ![]() . In fact these linearisations will
even vanish when we vary at a conformally flat metric.
. In fact these linearisations will
even vanish when we vary at a conformally flat metric.
Coming to the rescue of the situation is ![]() :
:
Exercise 4. Show that if ![]() is conformally invariant,
then its total metric variation tensor
is conformally invariant,
then its total metric variation tensor ![]() is conformally invariant.
Show that if
is conformally invariant.
Show that if ![]() is any conformally invariant tensor, then
the linearisation of the map
is any conformally invariant tensor, then
the linearisation of the map ![]() is conformally invariant
on trace-free perturbations of
is conformally invariant
on trace-free perturbations of ![]() (and 0 on pure trace perturbations).
(and 0 on pure trace perturbations).
Quantum considerations
Let ![]() be a natural differential operator with positive definite
leading symbol, and suppose
be a natural differential operator with positive definite
leading symbol, and suppose ![]() is a positive power of a conformally
invariant operator. For example,
is a positive power of a conformally
invariant operator. For example, ![]() could be one of the GJMS
operators, or it could be the square of the Dirac operator.
Then in dimensions 2,4,6, and conjecturally in higher even
dimensions,
could be one of the GJMS
operators, or it could be the square of the Dirac operator.
Then in dimensions 2,4,6, and conjecturally in higher even
dimensions,
Such formulas are the finite variational formulas corresponding to
Polyakov formulas, which are infinitesimal variational formulas
for the determinant; these take the form
In fact, getting from (![]() to (
to (![]() ))
may be viewed as a process of finding conformal primitives.
We say that a functional
))
may be viewed as a process of finding conformal primitives.
We say that a functional ![]() on the conformal class
on the conformal class ![]() is a conformal primitive for a local invariant
is a conformal primitive for a local invariant ![]() if
if
![]() . Of course this should happen at all possible
choices of background metric
. Of course this should happen at all possible
choices of background metric ![]() , and all directions of variation
, and all directions of variation
![]() . This can be said in a more invariant way, following
a suggestion of Mike Eastwood. Putting the
``running'' metric
. This can be said in a more invariant way, following
a suggestion of Mike Eastwood. Putting the
``running'' metric ![]() and the background metric on the same footing
in a two-metric functional
and the background metric on the same footing
in a two-metric functional
![]() on the conformal class, we
require of a conformal primitive that it be
on the conformal class, we
require of a conformal primitive that it be
Some local invariants have other local invariants as
conformal primitives. For example, since
In order to handle these objects more cleanly,
let's view ![]() and
and ![]() as being density-valued objects
as being density-valued objects ![]() and
and ![]() , so
that a ``weight term'' involving the conformal factor does not appear
explicitly. In other words, replace
, so
that a ``weight term'' involving the conformal factor does not appear
explicitly. In other words, replace ![]() by
by
![]() , and
, and
![]() by
by
![]() .
(For readers unfamiliar with densities, not much is lost conceptually
in assuming our manifold is oriented and talking about
.
(For readers unfamiliar with densities, not much is lost conceptually
in assuming our manifold is oriented and talking about ![]() -forms instead
of scalar densities.)
Then
-forms instead
of scalar densities.)
Then
Recall that when we wrote this, we were thinking about a background metric ![]() and a perturbed metric
and a perturbed metric ![]() .
But there
is an interesting way of rewriting the first term,
as
.
But there
is an interesting way of rewriting the first term,
as
Since the log-determinant functional will obviously satisfy the
cocycle condition (![]() ),
and since the second functional in (
),
and since the second functional in (![]() ) satisfies such a
condition, we expect
) satisfies such a
condition, we expect ![]() to behave similarly. One way to
see that this expectation is fulfilled is to use the conformal
primitive property: for fixed
to behave similarly. One way to
see that this expectation is fulfilled is to use the conformal
primitive property: for fixed ![]() and
and ![]() , with
, with ![]() for
for
![]() above, the two sides of (
above, the two sides of (![]() ) have the same conformal
variation (of
) have the same conformal
variation (of ![]() ), and the same value at
), and the same value at
![]() .
.
Exercise 5. Show that if ![]() ,
,
![]() ,
,
![]() , and
, and
![]() are 4 conformally
related metrics, then
are 4 conformally
related metrics, then
The following conjecture would be enough to prove the conjecture mentioned at the beginning of the section on the form of the determinant quotient.
Conjecture 1. If ![]() is a natural
is a natural ![]() -form and
-form and ![]() is
conformally invariant, then
is
conformally invariant, then
The point of separating these 3 kinds of terms is that
![]() will
have a very banal conformal primitive, namely itself, or (to write it
in a way that makes the properties of a conformal primitive more apparent),
will
have a very banal conformal primitive, namely itself, or (to write it
in a way that makes the properties of a conformal primitive more apparent),
Then there are the following related conjectures:
Conjecture 2. Any ![]() as above may be written
as above may be written
Conjecture 3. Any ![]() as above may be written
as above may be written
There are at least 2 filtrations of the local invariants of this type that
should be relevant. First, any invariant can be written as a sum of
monomial expressions in ![]() and
and ![]() with
with
![]() , where
, where
![]() (resp.
(resp. ![]() ) is the number of occurrences of
) is the number of occurrences of ![]() (resp.
(resp. ![]() )
in the monomial. If an invariant
)
in the monomial. If an invariant ![]() can be written with
can be written with
![]() for each monomial term, let's say
for each monomial term, let's say
![]() . Then
. Then
Exercise 6. Use the conformal change law for ![]() to show that
the class of
to show that
the class of ![]() in
in
![]() is nontrivial, and agrees with the class of
is nontrivial, and agrees with the class of
![]() .
This establishes that
Pff and
.
This establishes that
Pff and ![]() are ``at opposite ends'' of the
are ``at opposite ends'' of the ![]() -filtration.
-filtration.
The other filtration is by the degree of the conformal change law.
If
Other routes to ![]() and its variants
and its variants
There is an alternative definition of ![]() which avoids dimensional
continuation. We
write
which avoids dimensional
continuation. We
write ![]() for the space of smooth functions,
for the space of smooth functions,
![]() for space of smooth
1-forms and define the special section
for space of smooth
1-forms and define the special section
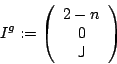
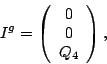
![\begin{displaymath}
\nabla_a \left(\begin{array}{c} \sigma \\ \mu \\ \tau \end{a...
...akebox[0.4em][l]{\tiny $\vert$}}{\sf {P}}\end{array}\right) .
\end{displaymath}](img197.gif)
This construction generalises. In each even dimension ![]() there is a
conformally invariant differential operator
there is a
conformally invariant differential operator
![]() so that
for any metric
so that
for any metric ![]() we have
we have
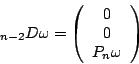
As a final comment on the above story we should clarify the origins of
the tractor field ![]() defined and used above. For those who are
familiar with tractors a more enlightening alternative definition is
defined and used above. For those who are
familiar with tractors a more enlightening alternative definition is
The main results above are derived via the ambient metric construction of
Fefferman and Graham. Explaining this construction would be a
significant detour at this point. Suffice to say that this
construction geometrically associates to an ![]() -dimensional conformal
manifold
-dimensional conformal
manifold ![]() an
an ![]() -dimensional pseudo-Riemannian manifold
-dimensional pseudo-Riemannian manifold
![]() . The GJMS operators
. The GJMS operators ![]() arise from powers of the
Laplacian
arise from powers of the
Laplacian
![]() , of
, of ![]() , acting on suitably
homogeneous functions. The operators
, acting on suitably
homogeneous functions. The operators
![]() arise in a similar
way from
arise in a similar
way from
![]() on appropriately homogeneous sections of
the tangent bundle
on appropriately homogeneous sections of
the tangent bundle ![]() . Such homogeneous sections correspond
to tractor fields on the conformal manifold
. Such homogeneous sections correspond
to tractor fields on the conformal manifold ![]() . The results above are
given by an easy calculation on the ambient manifold. Thus we can take
(
. The results above are
given by an easy calculation on the ambient manifold. Thus we can take
(![]() ) as a definition of the
) as a definition of the ![]() -curvature; it is simply the
natural scalar field that turns up on the right hand side.
-curvature; it is simply the
natural scalar field that turns up on the right hand side.
While this definition avoids dimensional continuation, there is still the issue of
getting a formula for ![]() . There is an effective algorithm for
re-expressing the ambient results in terms of tractors which then
expand easily into formulae in terms of the underlying Riemannian
curvature and its covariant derivatives. This solves the problem for small
. There is an effective algorithm for
re-expressing the ambient results in terms of tractors which then
expand easily into formulae in terms of the underlying Riemannian
curvature and its covariant derivatives. This solves the problem for small ![]() .
For example
.
For example
Problem 1: Give general formulae or inductive formulae
for the operators
![]() .
.
This seems to be a difficult problem. In another direction there is
another exercise to which we already have some answers. One of the
features of the ![]() -curvature is that it ``transforms by a linear operator''
within a conformal class.
More precisely, it is an example of a natural Riemannian tensor-density field
with a transformation law
-curvature is that it ``transforms by a linear operator''
within a conformal class.
More precisely, it is an example of a natural Riemannian tensor-density field
with a transformation law
Problem 2: Construct other natural tensor-densities which transform according
to (![]() ). (Note that any solution yields a conformally invariant natural operator
). (Note that any solution yields a conformally invariant natural operator ![]() .)
.)
From the transformation law for ![]() above, we can evidently
manufacture solutions to this problem. We have observed already that
above, we can evidently
manufacture solutions to this problem. We have observed already that
![]() is a section of the bundle
is a section of the bundle
![]() . If
. If ![]() is any scalar (or rather density) valued natural conformally invariant
differential operator which acts on
is any scalar (or rather density) valued natural conformally invariant
differential operator which acts on
![]() then
then ![]() can act on
can act on
![]() , and
, and ![]() has a conformal transformation of the the form
(
has a conformal transformation of the the form
(![]() ). Using the calculus naturally associated to
tractor bundles (or equally effectively,
using the ambient metric) it is in fact a
simple matter to write down examples, and the possibilities increase with
dimension.
This is most interesting when the resulting scalar field
gives a possible modification to the original
). Using the calculus naturally associated to
tractor bundles (or equally effectively,
using the ambient metric) it is in fact a
simple matter to write down examples, and the possibilities increase with
dimension.
This is most interesting when the resulting scalar field
gives a possible modification to the original ![]() -curvature. For those
familiar with densities this means that
-curvature. For those
familiar with densities this means that ![]() should take values in
densities of weight
should take values in
densities of weight ![]() ; this is the weight
at which densities that can be integrated
on a conformal manifold. For example, in any dimension we
may take
; this is the weight
at which densities that can be integrated
on a conformal manifold. For example, in any dimension we
may take ![]() to be
to be
![]() where
where ![]() indicates a contracted action of the tractor
indicates a contracted action of the tractor ![]() operator and the square of the Weyl curvature is here viewed as a
multiplication operator. In dimension
operator and the square of the Weyl curvature is here viewed as a
multiplication operator. In dimension ![]() this takes values in
this takes values in
![]() and we have
and we have
A generalisation: maps like ![]()
So far we have viewed the ![]() -curvature as a natural scalar field. It
turns out that if instead we view it as an operator then it fits
naturally into a bigger picture. To simplify matters suppose we are
working with a compact, oriented, but not necessarily
connected, manifold of even dimension
-curvature as a natural scalar field. It
turns out that if instead we view it as an operator then it fits
naturally into a bigger picture. To simplify matters suppose we are
working with a compact, oriented, but not necessarily
connected, manifold of even dimension ![]() .
We fix
.
We fix ![]() and so omit
and so omit ![]() in the notation for
in the notation for ![]() .
We can view
.
We can view ![]() as a multiplication operator from the closed 0-forms
as a multiplication operator from the closed 0-forms
![]() (i.e. the locally constant functions) into the space of
(i.e. the locally constant functions) into the space of ![]() -forms
-forms
![]() (which we identify with
(which we identify with
![]() via the conformal Hodge
via the conformal Hodge
![]() ). With the observations above we have the following properties:
). With the observations above we have the following properties:
The idea now is to look for analogous operators on other forms. We
write
![]() for the space of closed
for the space of closed ![]() -forms. Consider the operator
-forms. Consider the operator
Exercise 7.
On
![]() we have
we have
Note that the conformal variation term ![]() is the
Maxwell operator and is formally self-adjoint. So
is the
Maxwell operator and is formally self-adjoint. So ![]() satisfies the
analogue of property 1 above. The analogue of property 3 is an
immediate consequence, i.e.,
satisfies the
analogue of property 1 above. The analogue of property 3 is an
immediate consequence, i.e.,
![]() is
conformally invariant where now
is
conformally invariant where now ![]() is a closed
is a closed
![]() -form and
-form and
![]() (so in fact by compactness
(so in fact by compactness ![]() are both closed). Next observe, by inspection, that
are both closed). Next observe, by inspection, that ![]() is formally
self-adjoint. So we have analogues for 1,3,4. There is also a bonus
property, which is clear from the transformation law displayed:
is formally
self-adjoint. So we have analogues for 1,3,4. There is also a bonus
property, which is clear from the transformation law displayed:
So finally we need an analogue for
property 2. It is clear that ![]() is conformally invariant as a
map
is conformally invariant as a
map
![]() ,
so this is an analogue. But we can do more.
There is no reason to
suppose the image is co-closed.
On the other hand note that
,
so this is an analogue. But we can do more.
There is no reason to
suppose the image is co-closed.
On the other hand note that ![]() is conformally invariant on
is conformally invariant on
![]() and so
we have the following:
and so
we have the following:
Fact: Let
![]() , where
, where ![]() ,
, ![]() , with
the standard Riemannian structure.
Then
, with
the standard Riemannian structure.
Then
![]() if and only if
if and only if ![]() is harmonic.
Furthermore,
the map (
is harmonic.
Furthermore,
the map (![]() ) is non-trivial.
) is non-trivial.
In some recent work the authors have used the
ambient metric, and its relationship to tractors,
to show that the above construction generalises along the following lines:
There are operators
![]() (
(![]() ), given
by a uniform construction, with the following properties:
), given
by a uniform construction, with the following properties:
Problems ![]() : There are analogues for the operators
: There are analogues for the operators ![]() of most of the conundrums and problems for the
of most of the conundrums and problems for the ![]() -curvature.
-curvature.
Back to the
main index
for Conformal structure in Geometry, Analysis, and Physics .