Mean values of shifted zeta-functions

Recently Conrey, Farmer, Keating, and Snaith have conjectured mean values for products of zeta functions shifted off the $\frac12$-line. The integrals they consider are of the form

$$\int_0^T \prod_{j=1}^J \zeta(\frac12 + a_j + \epsilon_j t)\ dt ,$$

where $\epsilon_j=\pm 1$. They have shown that it is possible to use Dirichlet polynomial techniques to conjecture the full main term for the above mean value, and it is also possible to exactly evaluate the analogous expression involving characteristic ploynomials of matrices from the CUE. The two calculations agree in every term, apart from arithmetic factors which are not incorporated into the randon matrix model.

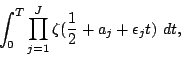
These techniques extend to the case of ratios of zeta functions, and also are applicable to mean values of $L$-functions with other symmetry types.

(A more extensive description is in preparation).

Back to the main index for L-functions and Random Matrix Theory.