Graph catalog: Families of graphs
Version: March 1, 2007
Index of families of graphs
Main Index
Index of graphs
Description of graph entries
Graph operations
Parameter relationships
References
The catalog
This catalog provides information about the minimum rank and other graph
parameters for families of connected graphs. The description of a family
of graphs involves one or more parameters (often the order n of the
graph).
For specific small graphs, please consult the
Graph
catalog: Small graphs.
For general background on the minimum
rank problem, please see [FH]. Proofs of
the results in the catalog can be found in the references
cited in the catalog.
This catalog was developed through the American Institute of Mathematics
workshop, "Spectra of Families of Matrices described by Graphs, Digraphs,
and Sign Patterns," and is hosted by the AIM web-site. It is edited by
Wayne Barrett, Leslie Hogben, and Hein van der Holst.
The web-page was designed by David Farmer.
Please refer any questions or comments about the content of the catalog,
including corrections or suggestions for additional information, to
Leslie Hogben (lhogben(())iastate.edu).
Please refer any questions or comments about the operation of this web-site
to David Farmer (farmer(())aimath.org).
AIM workshop participants:
Francesco Barioli, Wayne Barrett, Avi Berman,
Richard Brualdi, Steven Butler,
Sebastian Cioaba, Dragos Cvetkovic, Jane Day,
Louis Deaett, Luz DeAlba, Shaun Fallat, Shmuel Friedland,
Chris Godsil, Jason Grout, Willem Haemers, Leslie Hogben,
In-Jae Kim, Steve Kirkland, Raphael Loewy, Judith McDonald,
Rana Mikkelson,
Sivaram Narayan, Olga Pryporova, Uri Rothblum, Irene Sciriha,
Bryan Shader, Wasin So, Dragan Stevanovic, Pauline van den Driessche,
Hein van der Holst, Kevin Vander Meulen, Amy Wangsness, Amy Yielding.
Entries in the catalog
A typical entry in this catalog includes the following information
for the graph or family of graphs.
| Symbol name |
Common names/symbols are used to describe a graph G in the family.
Sometimes a graph operation is used.
|
|
picture |
A picture of the graph, or a representative example from the family.
|
| order | The number of vertices in the graph
|
| mr |
For a real symmetric matrix A, the graph of A,
denoted G(A), is the graph with vertices
{1,...,n } and edges { {i,j } | aij ≠ 0 and i
≠ j }
(note that the diagonal of A is ignored in determining G(A)).
The minimum rank of G is
mr(G)=min{rank(A) : A ∈ Rn, AT=A, and G(A)=G}.
|
| M |
The maximum nullity (= maximum multiplicity of an eigenvalue) of a real symmetric matrix A such that G(A)=G
|
| field independent |
Minimum rank can be defined for symmetric matrices over any field. ``Yes" means the minimum rank of G is the same for all fields.
|
| ξ |
A real symmetric matrix M satisfies the Strong Arnold
Hypothesis provided there does not exist a nonzero symmetric matrix
X satisfying:
- MX = 0,
- M ° X = 0,
- I ° X=0,
where ° denotes the Hadamard (entrywise) product and I is the identity matrix.
The Colin de Veriere-type parameter ξ(G) is the maximum multiplicity of 0 as an eigenvalue
among symmetric real matrices that satisfy
- G(A )=G and
- A satisfies the Strong Arnold Hypothesis.
|
| ω |
The largest value of m for which G has a clique of order m (subgraph isomorphic to Km) is called the clique number of G
and denoted by ω(G).
|
| δ |
The minimum degree of a vertex of G is denoted by δ(G).
|
| tw |
A tree-decomposition of a graph G=(V,E) is a pair
(T,W), where T is a tree and W={Wt : t∈ V(T)} is a family of subsets of V
with the properties:
- ∪ {Wt : t∈ V(T)}=V,
- for every edge e∈ E, there is a t∈V(T) such that has both ends of e are in Wt, and
- if t1,t2,t3∈ V(T)
and t2 lies on the path from t1 to t3 in T, then
Wt1∩Wt3⊆Wt2.
The width of a tree-decomposition is
max{|Wt| - 1 : t∈ V(T)}. The tree-width of G, denoted by tw(G), is the minimum possible width of a tree-decomposition of G.
|
| cc |
Clique covering number, or Cliquecover.
A set of subgraphs of G, each of which is a clique and such that every edge of G is
contained in at least one of these cliques, is called a clique covering of G.
The clique covering number of G, denoted by cc(G), is the smallest number of
cliques in a clique covering of G.
|
| diam |
The distance between two vertices in a graph G is the
number of edges in a shortest path between them.
The diameter of G, diam(G), is the maximum distance between any two vertices
of G.
|
| maxinducedpath |
The maximum number of edges in a path that is an induced subgraph of G.
|
| Z |
Color-change rule:
If G is a graph with each vertex colored either white or black, u is a black vertex of G, and exactly one neighbor v of u is white, then change the color of v to black.
Given a coloring of G, the derived coloring is the result of applying the color-change rule until no more changes result.
A zero forcing set for a graph G is a subset of vertices Z such that if initially the vertices in Z are colored black and the remaining vertices are colored white, the derived coloring of G is all black.
Z(G) is the minimum of |Z| over all zero forcing sets Z⊆ V(G).
|
| α |
An induced subgraph H of a graph G
is a coclique or independent set of vertices
if H has no edges.
The largest value of m for which a coclique with m
vertices exists is called the vertex independence number
of G and denoted by α(G).
|
|
| Notes: |
Any other comments.
|
Graph operations
The following graph operations are used to construct families:
- The complement of a graph G=(V,E) is the
graph G
= (V,E),
where E
consists of all two element sets from V that are not in E.
- The line graph of a graph G=(V,E),
denoted L(G), is the graph having vertex set E,
with two vertices in L(G) adjacent if and only if the
corresponding edges are adjacent in G.
- The Cartesian product of two graphs G and H,
denoted G ☐ H,
is the graph with vertex set V(G) × V(H) such that
(u,v) is adjacent to (u',v') if and only if
(1) u=u' and vv' ∈ E(H),
or
(2) v=v' and uu' ∈ E(G).
- The strong product of two graphs G and H, denoted
G ⊠ H, is the graph with vertex set V(G) × V(H) such
that (u,v) is adjacent to (u',v') if and only if
(1) uu' ∈ E(G)
and vv' ∈ E(H),
or
(2) u=u' and vv' ∈ E(H),
or
(3) v=v'
and uu' ∈ E(G).
- The corona of G with H, denoted
G ° H, is the graph of order |G||H| + |G|
obtained by taking one copy of G and |G| copies
of H, and joining all the vertices in the ith
copy of H to the ith vertex of G.
Parameter Relationships
The following relationships between the parameters are known:
- mr(G) + M(G) = |G| (where |G| denotes the order of G)
- M(G) ≤ Z(G) [AIM]
- ξ(G) ≤ M(G) [BFH3]
- ω(G) -1 ≤ ξ(G) [BFH3]
- δ(G) ≤ tw(G)
- mr(G) ≤ cc(G)
- diam(G) ≤ maxinducedpath(G) ≤ mr(G)
- ξ(G) ≤ |G| - α(G) + 1 [BFH3]
References
[AIM] AIM Minimum rank - special graphs work group. Zero forcing sets and the minimum rank of graphs. Preprint.
[BFH] F. Barioli, S. Fallat, and L. Hogben.
Computation of minimal rank and path cover number for graphs.
Linear Algebra and Its Applications,
392: 289--303, 2004.
[BFH2] F. Barioli, S. Fallat, and L. Hogben.
On the difference between the maximum multiplicity and path cover number for
tree-like graphs.
Linear Algebra and Its Applications 409: 13--31, 2005.
[BFH3] F. Barioli, S. Fallat, and L. Hogben.
A variant on the graph parameters of Colin de Verdi`ere:
Implications to the minimum rank of graphs.
Electronic Journal of Linear Algebra,
13: 387--404, 2005.
[BHL] W. Barrett, H. van der Holst and R. Loewy.
Graphs whose minimal rank is two.
Electronic Journal of Linear Algebra,
11: 258--280, 2004.
[FH] S. Fallat and L. Hogben.
The Minimum Rank of Symmetric Matrices Described by a Graph: A Survey. Preprint.
[H] L. Hogben.
Spectral graph theory and the inverse eigenvalue problem of a
graph.
Electronic Journal of Linear Algebra, 14:12-31, 2005.
[HvdH] L. Hogben and H. van der Holst.
Forbidden minors for the class of graphs G with
ξ(G) ≤ 2. To appear in Linear Algebra and Its Applications.
[JLD] C. R. Johnson and A. Leal Duarte.
The maximum multiplicity of an eigenvalue in a matrix whose graph is a tree.
Linear and Multilinear Algebra 46: 139--144, 1999.
[JS] C. R. Johnson and C. M. Saiago.
Estimation of the maximum multiplicity of an eigenvalue in terms of the vertex degrees
of the graph of the matrix.
Electronic Journal of Linear Algebra,
9:27--31, 2002.
Catalog of graphs
 path on
path on  vertices
vertices
|
| Order : | 
| | mr : | 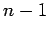
| | M : | 1 | | field independent : | yes | | ξ : | 1 | | ω : | 2 | | δ : | 1 | | tw : | 1 | | cc : | 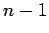
| | Diameter : | 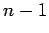
| | maxinducedpath : | 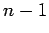
| | Z : | 1 | | α : |
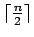
| | Notes : | 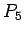 is displayed.
is displayed.
|
| 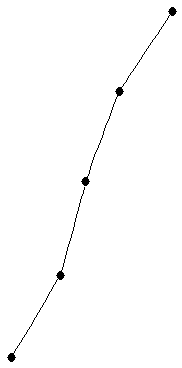 |
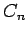
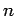 -cycle
-cycle
|
| Order : | 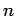
| | mr : | 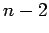
| | M : | 2 | | field independent : | yes | | ξ : | 2 | | ω : | 2 | | δ : | 2 | | tw : | 2 | | cc : | 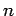
| | Diameter : |
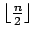
| | maxinducedpath : | 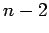
| | Z : | 2 | | α : |
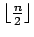
| | Notes : | 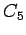 is displayed.
is displayed. 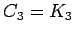 .
.
|
| 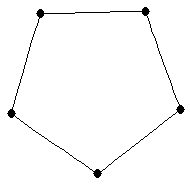 |
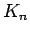 complete graph on
complete graph on 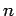 vertices
vertices
|
| Order : | 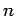
| | mr : | 1 | | M : | 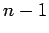
| | field independent : | yes | | ξ : | 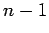
| | ω : | 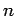
| | δ : | 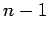
| | tw : | 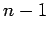
| | cc : | 1 | | Diameter : | 1 | | maxinducedpath : | 1 | | Z : | 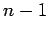
| | α : | 1 | | Notes : | 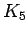 is displayed.
is displayed.
|
| 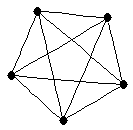 |
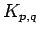 complete bipartite graph on
complete bipartite graph on 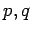 vertices
vertices
|
| Order : | 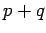
| | mr : | 2 | | M : | 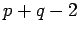
| | field independent : | yes | | ξ : |
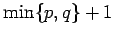 (for
(for
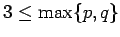 )
)
| | ω : | 2 | | δ : |
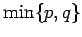
| | cc : | 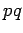
| | Diameter : | 2 | | maxinducedpath : | 2 | | Z : | 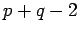
| | α : |
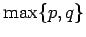
| | Notes : | 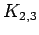 is displayed.
is displayed.
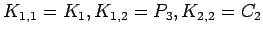 .
.
|
| 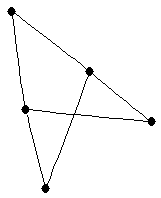 |
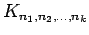 Complete multipartite graph
Complete multipartite graph |
| Order : |
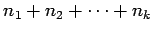
| | mr : |
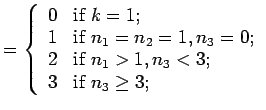
| | field independent : | no | | δ : |
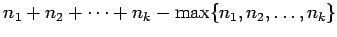
| | Notes : |
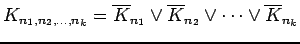 where
where
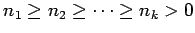 .
.
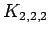 is shown.
is shown.
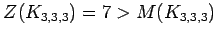 .
.
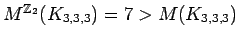 .
.
References:[BvdHL04], [FH]
|
| 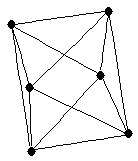 |
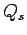
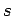 th hypercube
th hypercube
|
| Order : | 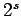
| | mr : |
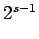
| | M : |
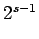
| | ω : | 2 | | δ : | 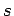
| | cc : |
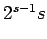 (= # edges)
(= # edges)
| | Diameter : | 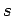
| | Z : |
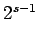
| | α : |
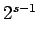
| | Notes : | 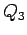 is displayed.
is displayed.
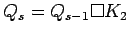 .
.
Reference:[AIM]
|
| 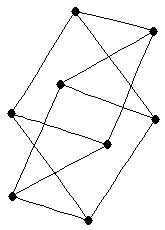 |
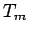
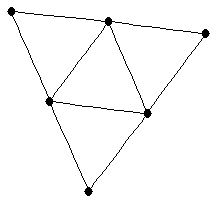
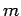 th supertriangle
th supertriangle
|
| Order : |
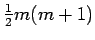
| | mr : |
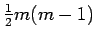
| | M : | 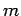
| | ξ : | 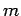
| | ω : | 3 | | δ : | 2 | | cc : |
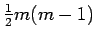
| | Diameter : | 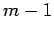
| | Z : | 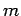
| | Notes : | 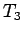 is shown.
is shown.
minimum rank is same for all infinite fields.
Reference: [AIM]
|
|  |
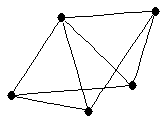
 wheel on
wheel on 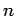 vertices
vertices
|
| Order : | 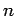
| | mr : | 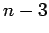
| | M : | 3 | | field independent : | no (see notes) | | ξ : | 3 | | ω : | 3 | | δ : | 3 | | tw : | 3 | | cc : | 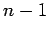
| | Diameter : | 2 | | maxinducedpath : | 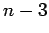
| | Z : | 3 | | α : |
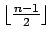
| | Notes : | 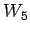 is displayed.
is displayed.
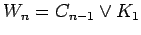 .
.
mr
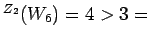 mr
mr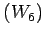 .
.
References: [H]; [BFH05a, Thm 3.16] for 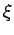 .
.
|
|  |
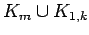
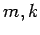 -pineapple (
-pineapple (
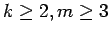 )
)
|
| Order : | 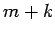
| | mr : | 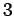
| | M : | 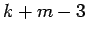
| | field independent : | yes | | ω : | 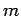
| | δ : | 1 | | cc : | 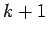
| | Diameter : | 2 | | maxinducedpath : | 2 | | Z : | 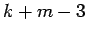
| | α : | 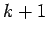
| | Notes : | The 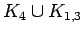 -pineapple is
-pineapple is
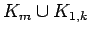 where the intersection is the single vertex
where the intersection is the single vertex 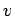 .
.
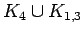 is shown.
is shown.
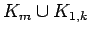 can be covered by
can be covered by 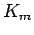 and
and 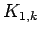 , so mr
, so mr
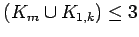 .
.
All vertices of 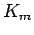 except
except  and one other, together with all but one of the
and one other, together with all but one of the 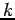 vertices of degree 1, is a zero forcing set.
vertices of degree 1, is a zero forcing set.
|
| 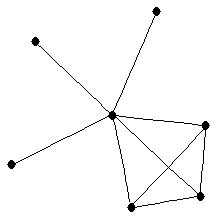 |
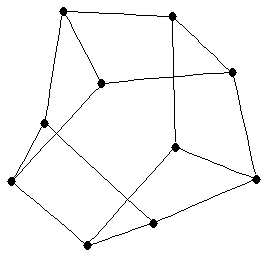
| Moebius ladder |
| Order : | 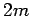
| | mr : | 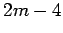
| | M : | 4 | | ξ : | 4 | | ω : | 2 | | δ : | 3 | | cc : | 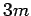 (= # edges)
(= # edges)
| | Z : | 4 | | Notes : | 5th Möbius ladder is shown.
Reference: [AIM]
|
|  |
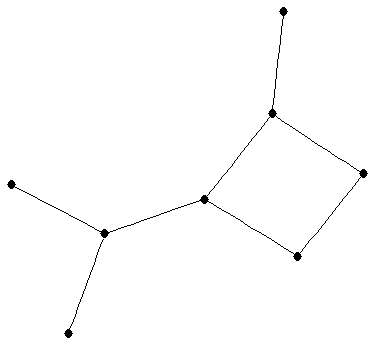
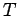 tree
tree |
| mr : |
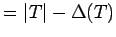
| | M : |
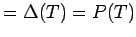
| | field independent : | yes | | ξ : | 2 (for 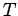 not a path)
not a path)
| | ω : | 2 | | δ : | 1 | | tw : | 1 | | cc : | 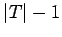
| | Z : | 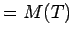
| | Notes : |
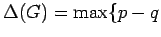 : there is a set of : there is a set of 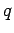 vertices whose deletion leaves vertices whose deletion leaves 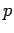 paths} paths}
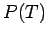 = path cover number.
= path cover number.
References: [JLD];
for algorithms for computation of 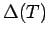 , see [JS] or [FH]; for
, see [JS] or [FH]; for 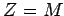 , see [AIM]; for
, see [AIM]; for 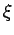 see [BFH3].
see [BFH3].
|
| 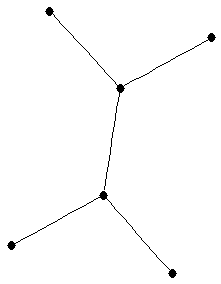 |
| linear 2-tree |
| mr : | 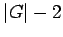
| | M : | 2 | | field independent : | yes | | ξ : | 2 | | δ : | 2 | | Z : | 2 | | Notes : | A linear 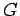 -tree is a
-tree is a 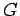 -connected graph
-connected graph 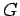 that can be embedded
in the plane such that the graph obtained from the dual of
that can be embedded
in the plane such that the graph obtained from the dual of 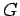 after
deleting the
vertex corresponding to the infinite face is a path.
after
deleting the
vertex corresponding to the infinite face is a path.
Reference: [HvdH07]
|
| 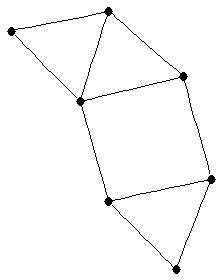 |
| claw-free block-clique (1-chordal) graph |
| mr : | = cliquecover(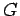 )
)
| | M : |
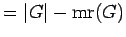
| | field independent : | yes | | cc : | # of blocks | | Z : | 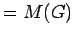
| | Notes : | For the block-clique graph  shown,
shown,
mr( )=4.
)=4.
This result requires claw-free or equivalently no vertex in more than 2 blocks.
A claw-free block-clique is the line graph of a tree.
reference: [AIM]
|
|  |
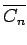 complement of
complement of 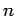 -cycle
-cycle
|
| Order : |
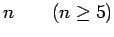
| | mr : | 3 | | M : | 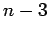
| | field independent : | no (see notes) | | ω : |
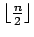
| | δ : | 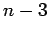
| | Diameter : | 2 | | maxinducedpath : | 3 | | Z : | 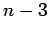
| | α : | 2 | | Notes : |
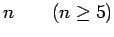
|
| 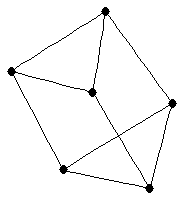 |
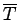 complement of a tree
complement of a tree |
| mr : |
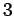 if if 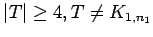
| | M : |
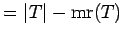
| | maxinducedpath : | 3 if
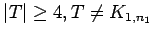
| | Z : |
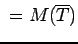
| | α : | 2 | | Notes : |
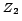 .
.
Reference: [AIM]
|
| 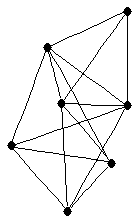 |
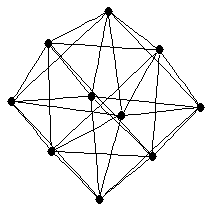
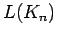 line graph of complete graph
line graph of complete graph |
| Order : |
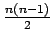
| | mr : | 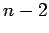
| | M : |
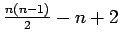
| | δ : | 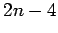
| | Diameter : | 2 | | Z : |
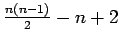
| | Notes : | 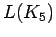 is shown
is shown
Reference: [AIM]
|
|  |
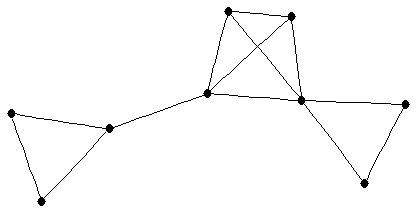
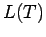 line graph of a tree
line graph of a tree |
| Order : | 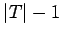
| | mr : | 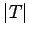 - number of pendent vertices of
- number of pendent vertices of 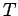
| | M : | number of pendent vertices of 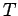 - 1
- 1
| | field independent : | yes | | ω : | maximum degree of vertex of 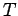
| | cc : | 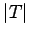 - number of pendent vertices of
- number of pendent vertices of 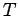
| | Z : | number of pendent vertices of 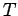 - 1
- 1
| | Notes : | Reference: [AIM]
|
|  |
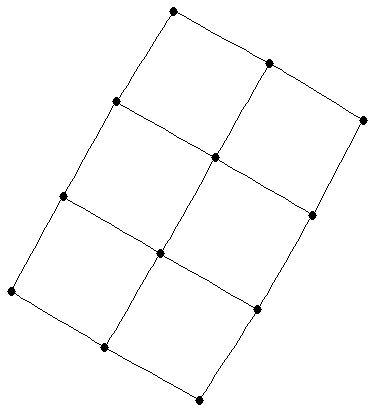
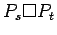 Cartesian product of two paths
Cartesian product of two paths |
| Order : | 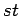
| | mr : |
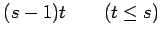
| | M : |
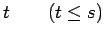
| | ω : | 2 | | δ : | 2 | | cc : | = # of edges | | Diameter : | 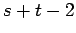
| | Z : |
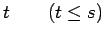
| | Notes : |
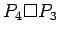 is shown
is shown
Reference: [AIM]
|
|  |
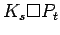 Cartesian product of a complete graph and a path
Cartesian product of a complete graph and a path |
| Order : | 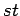
| | mr : | 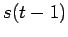
| | M : | 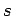
| | field independent : | no (see notes) | | ξ : | 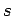
| | ω : | 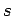
| | δ : | 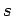
| | cc : | 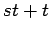
| | Diameter : | 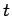
| | maxinducedpath : |
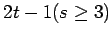
| | Z : | 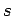
| | α : | 2 | | Notes : |
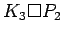 is displayed.
is displayed.
Minimum rank over 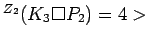 is different
is different
References: [AIM]
|
| 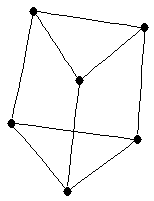 |
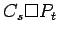 Cartesian product of a cycle and a path
Cartesian product of a cycle and a path |
| Order : | 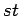
| | mr : |
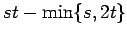
| | M : |
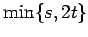
| | ω : | 2 (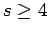 )
)
| | δ : | 3 | | cc : | = # of edges (if 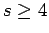 )
)
| | Diameter : |
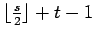
| | Z : |
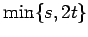
| | Notes : |
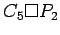 is shown.
is shown.
Reference: [AIM]
|
| 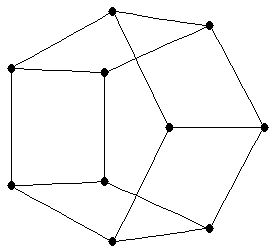 |
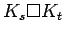 cartesian product of two complete graphs
cartesian product of two complete graphs |
| Order : | 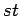
| | mr : | 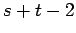
| | M : | 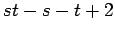
| | ω : | 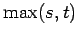
| | δ : | 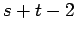
| | Z : | 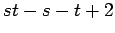
| | Notes : |
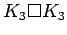 is shown.
is shown.
Reference: [AIM]
|
| 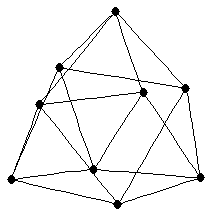 |
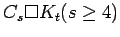 Cartesian product of a cycle and a complete graph
Cartesian product of a cycle and a complete graph |
| Order : | 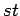
| | mr : | 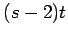
| | M : | 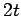
| | ω : | 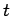
| | δ : | 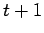
| | Z : | 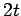
| | Notes : |
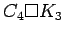 is shown.
is shown.
Reference: [AIM]
|
| 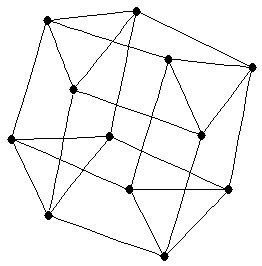 |
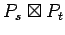 strong product of two paths
strong product of two paths |
| Order : | 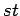
| | mr : |
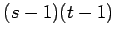
| | M : | 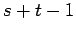
| | ω : | 4 | | δ : | 3 | | cc : |
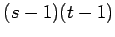
| | Diameter : |
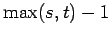
| | Z : | 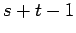
| | Notes : |
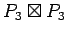 is shown.
is shown.
minimum rank same for all infinite fields
Reference: [AIM]
|
|  |
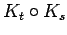 corona of
corona of 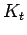 by
by 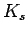 (
(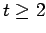 )
)
|
| Order : | 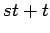
| | mr : | 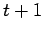
| | M : | 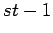
| | field independent : | yes | | ω : |
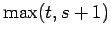
| | δ : | 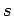
| | cc : | 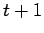
| | Diameter : | 3 | | maxinducedpath : | 3 | | Z : | 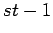
| | α : | 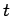
| | Notes : |
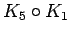 is shown
is shown
References: [AIM]
|
| 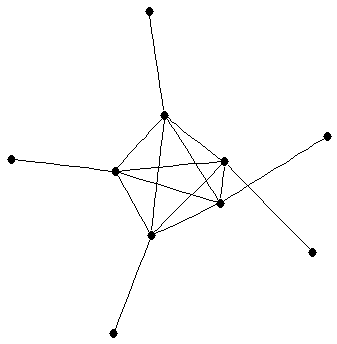 |
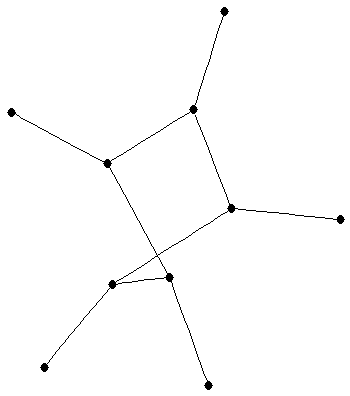
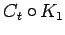 corona of
corona of 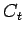 with
with 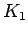 (
(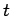 -sun)
-sun)
|
| Order : | 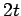
| | mr : |
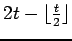 (for
(for 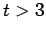 )
)
| | M : |
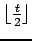 (for
(for 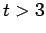 )
)
| | field independent : | yes | | ω : | 2 (for 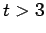 )
)
| | δ : | 1 | | tw : | 2 | | cc : | 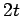 (for
(for 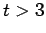 )
)
| | Diameter : |
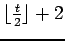
| | maxinducedpath : | 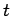
| | α : | 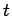
| | Notes : |
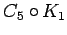 is displayed.
is displayed.
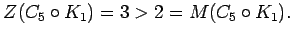
mr(
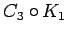 )=4.
)=4.
References: [BFH04] and [BFH05]
|
|  |
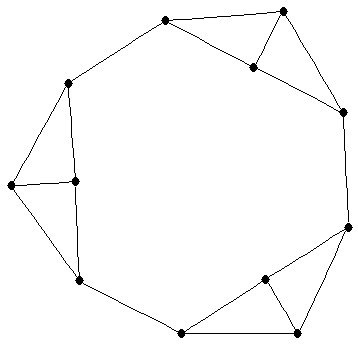
| necklace |
| Order : | 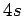
| | mr : | 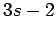
| | M : | 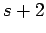
| | ω : | 3 | | δ : | 3 | | cc : | 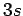
| | maxinducedpath : | 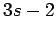
| | Z : | 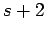
| | Notes : | The necklace with 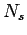 diamonds is a 3-regular graph that can be constructed from a
diamonds is a 3-regular graph that can be constructed from a 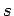 -cycle by appending
-cycle by appending 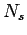 extra vertices. Each "extra" vertex is adjacent to 3 sequential cycle vertices. The adjacency matrix + I achieve minimum rank.
extra vertices. Each "extra" vertex is adjacent to 3 sequential cycle vertices. The adjacency matrix + I achieve minimum rank.
|
|  |