A map of topological spaces
 is a homology
fibration if, for every
is a homology
fibration if, for every 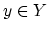 , the natural map
, the natural map
 from the fiber over
from the fiber over 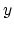 to the homotopy fiber over
to the homotopy fiber over
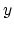 induces an isomorphism on homology groups. By a theorem of McDuff
and Segal, this is implied, for instance, by the condition that for
sufficiently small neighborhoods
induces an isomorphism on homology groups. By a theorem of McDuff
and Segal, this is implied, for instance, by the condition that for
sufficiently small neighborhoods 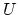 of
of 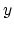 , the inclusion
, the inclusion
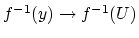 induces an isomorphism on homology.
induces an isomorphism on homology.
Jeffrey Herschel Giansiracusa
2005-05-17