Hurwitz numbers give a count of genus  , degree
, degree  covers of
covers of
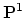 with ramification profile
with ramification profile
 over fixed branch points
over fixed branch points
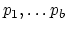 . Covers with
automorphism group
. Covers with
automorphism group  are counted with weight
are counted with weight 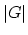 . The Hurwitz
numbers can be calculated explicitly in terms of the character theory
of the symmetric group. Remarkably, they can also be expressed in
terms of tautological integrals on
. The Hurwitz
numbers can be calculated explicitly in terms of the character theory
of the symmetric group. Remarkably, they can also be expressed in
terms of tautological integrals on
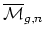 by the ELSV formula (see references below).
by the ELSV formula (see references below).
Ekedahl, Lando, Shapiro, Vainshtein, On Hurwitz numbers
and Hodge integrals. C. R. Acad. Sci. Paris SÚr. I Math. 328
(1999), no. 12, 1175-1180.
Hurwitz numbers and intersections on moduli spaces of curves.
Invent. Math. 146 (2001), no. 2, 297-327.
Jeffrey Herschel Giansiracusa
2005-05-17