The arithmetic genus of an
irreducible, projective curve 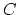 is
is
 where
where
 is the structure sheaf of holomorphic functions on
is the structure sheaf of holomorphic functions on
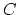 . For a smooth curve, this is the same as the geometric genus;
however, unlike the geometric genus, the arithmetic genus has the nice
feature that it remains constant in families of curves with possibly
singular fibers. Intuitively this means that the arithmetic genus of a
nodal curve is the geometric genus of the curve obtained by smoothing
out the nodes.
. For a smooth curve, this is the same as the geometric genus;
however, unlike the geometric genus, the arithmetic genus has the nice
feature that it remains constant in families of curves with possibly
singular fibers. Intuitively this means that the arithmetic genus of a
nodal curve is the geometric genus of the curve obtained by smoothing
out the nodes.
Jeffrey Herschel Giansiracusa
2005-05-17