The tautological ring
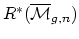 is the subring of the the Chow
ring
is the subring of the the Chow
ring
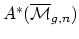 which is meant to contain all of the natural
geometric information. Faber and Pandharipande gave the following
elegant formulation (which is equivalent to previous definitions). There
are forgetful morphisms
which is meant to contain all of the natural
geometric information. Faber and Pandharipande gave the following
elegant formulation (which is equivalent to previous definitions). There
are forgetful morphisms
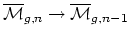 and gluing
morphisms
and gluing
morphisms
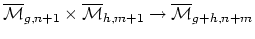 and
and
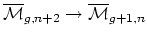 . The system of tautological rings is
then the smallest system of
. The system of tautological rings is
then the smallest system of
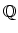 -subalgebras of the Chow rings
which is closed under the gluing and pushforward maps and which
contains all of the Witten classes
-subalgebras of the Chow rings
which is closed under the gluing and pushforward maps and which
contains all of the Witten classes 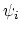 . Tautological rings for
the uncompactified moduli space and its partial compactifications are
defined by restriction.
. Tautological rings for
the uncompactified moduli space and its partial compactifications are
defined by restriction.
Jeffrey Herschel Giansiracusa
2005-06-27