Teichmuller space
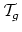 for genus
for genus 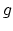 parametrizes pairs
parametrizes pairs
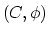 of a genus
of a genus 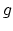 Riemann surface
Riemann surface 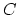 and a homeomorphism
and a homeomorphism
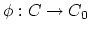 to a fixed surface of genus
to a fixed surface of genus 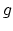 , up to
isotopy of
, up to
isotopy of 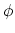 . This is equivalent to parametrizing Riemann
surfaces
. This is equivalent to parametrizing Riemann
surfaces 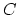 with a choice of normalized generators of
with a choice of normalized generators of
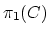 .
It is naturally an open subset of
.
It is naturally an open subset of
 , homeomorphic to
a ball. It admits an action of the mapping class group
, homeomorphic to
a ball. It admits an action of the mapping class group 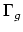 with finite stabilizers and with quotient
with finite stabilizers and with quotient
 .
.
Jeffrey Herschel Giansiracusa
2005-06-27